BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Up: AC Circuits
Previous: The Differential Equation
From the point of view of the power supply,21.5
the circuit is a "black box" that "resists" the applied voltage
with a rather weird "back
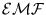 "
"
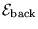 given by
given by
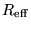 times the current I;
times the current I;
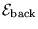 is given by the sum of all three terms in Eq. (13)
or the sum of the three vectors in Fig. 21.2.
The power dissipated in the circuit is
the product of the real part of the applied voltage21.6
and the real part of the resultant current21.7
is given by the sum of all three terms in Eq. (13)
or the sum of the three vectors in Fig. 21.2.
The power dissipated in the circuit is
the product of the real part of the applied voltage21.6
and the real part of the resultant current21.7
| P(t) |
= |
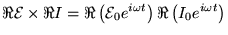 |
(21.14) |
which oscillates at a frequency 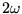 between zero and its maximum value
between zero and its maximum value
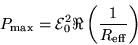 |
(21.15) |
so that the average power drain is21.8
![\begin{displaymath}\langle P \rangle = {1\over2} {\cal E}_0^2
\left[ R \over R^2 + (X_L - X_C)^2 \right] \; .
\end{displaymath}](img39.gif) |
(21.16) |
A variation on this algebra yields the practical formula
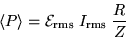 |
(21.17) |
where
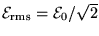 ,
,
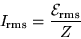 |
(21.18) |
is the root-mean-square current in the circuit,
R/Z is the "power factor" of the RC circuit and
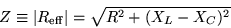 |
(21.19) |
is the impedance of the circuit.21.9


Up: AC Circuits
Previous: The Differential Equation
Jess H. Brewer -
Last modified: Mon Nov 16 18:21:16 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE