Static Zero Field Relaxation

Relaxonomy --> here

---

By convention we define the muon spin polarization <math>\vec{P}</math> to be initially in the <math>\hat{z}</math> direction when there is no applied magnetic field (ZF). The relaxation of <math>\vec{P}</math> is then described by

<math> g_{zz}(t) \; \equiv \; \langle P_z(0) \, P_z(t) \rangle \; , </math>

where the lower case <math>g_{zz}(t)</math> denotes the static case of the more general <math>G_{zz}(t)</math> relaxation function.

Like "relaxation" in TF, this formulation suffers from several assumptions that are frequently invalid: first, that the average local magnetic field <math>\langle \vec{B_\mu} \rangle</math> at the muons is also zero; second, that any random local magnetic fields (RLMF) <math>\vec{B_\mu}</math> are distributed uniformly about zero in all three directions. The first assumption is not true for a magnetized ferromagnetic crystal, for example, and the second is probably not true in any single crystal environment with RLMF. In such cases this description is strictly invalid, but people use it as an approximation anyway.

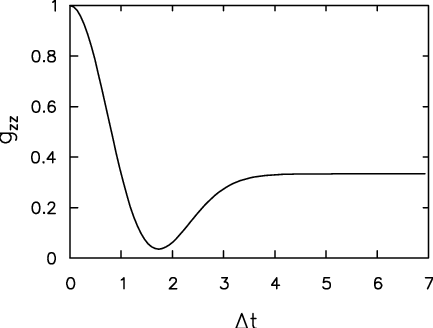
For the case of an isotropically random local field with a Gaussian width <math>\Delta</math>,

<math>{\cal D}(|B|) = {1 \over \sqrt{2\pi} \; \Delta} \exp\left[- {1\over2} \left(B \over \Delta \right)^2\right] </math>,

the resultant "Kubo-Toyabe" static ZF relaxation function (named after Kubo and Toyabe, who first described it) looks like this:

<math>g_{zz}^G(\Delta,t) = {1\over3} + {2\over3} \exp\left[{1\over2}\Delta^2 t^2\right]\left(1 - \Delta^2 t^2\right)</math>.