THE UNIVERSITY OF BRITISH COLUMBIA
Physics 108
Assignment #
8:
FARADAY & INDUCTANCE
Wed. 2 Mar. 2005 - finish by Wed. 9 Mar.
- Earth's-Field Generator:
What is the maximum that can be induced in a circular coil of
5000 turns and radius 50 cm by rotating it 30
times per second in the Earth's magnetic field in Vancouver
(
 T)?
T)?
-
Triangular Loop:
A wire loop in the shape of an equilateral triangle
(length of a side
 m)
travelling at a constant speed
m)
travelling at a constant speed  m/s
moves, "pointy" end first, into a region
where a uniform magnetic field
m/s
moves, "pointy" end first, into a region
where a uniform magnetic field  T
points into the paper, as shown.
T
points into the paper, as shown.
- Does current flow clockwise or counterclockwise
(or not at all)
around the triangular loop as it enters the field?
- What is the maximum induced
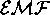 around the loop
as it enters the field?
around the loop
as it enters the field?
- Sketch the induced
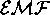 around the loop
around the loop
as a function of time, from the time it begins to enter the field
until it is entirely in the field.
around the loop
around the loop
as a function of time, from the time it begins to enter the field
until it is entirely in the field.
-
Moving Loop in Non-Uniform Field:
A long, straight, stationary wire carries a constant current of
150 A. Nearby abcd, a square loop 12 cm on a side,
is moving away from the stationary wire
(in a direction perpendicular to the wire)
at a speed of
 m/s.
The long wire and the sides of the loop are all in a common plane;
the near (ab) and far (cd) sides of the loop
are parallel to the long wire and the other two sides
(bc and da) are perpendicular to it.
The near side (ab) is initially
m/s.
The long wire and the sides of the loop are all in a common plane;
the near (ab) and far (cd) sides of the loop
are parallel to the long wire and the other two sides
(bc and da) are perpendicular to it.
The near side (ab) is initially  cm
away from the long wire.
Calculate the around the square loop at this instant,
assuming that the resistance of the loop is large enough that
any actual current flowing around it produces a negligible magnetic flux.
Also indicate the direction of the small current in side cd.
cm
away from the long wire.
Calculate the around the square loop at this instant,
assuming that the resistance of the loop is large enough that
any actual current flowing around it produces a negligible magnetic flux.
Also indicate the direction of the small current in side cd.
Challenge Problem
for Extra Credit
[20 marks]
Dropping Frame:
A square metallic frame is located, as shown, between the poles of an
electromagnet, with its face perpendicular to
 .
The upper side is in a region of effectively uniform field with magnitude
.
The upper side is in a region of effectively uniform field with magnitude
 T, while the lower side is outside the gap, where the field
is essentially zero.
If the frame is released and falls under its own weight,
determine the downward terminal velocity.
Assume the frame is made of aluminum
(density 2.7 g/cm
T, while the lower side is outside the gap, where the field
is essentially zero.
If the frame is released and falls under its own weight,
determine the downward terminal velocity.
Assume the frame is made of aluminum
(density 2.7 g/cm and
resistivity
and
resistivity

 -cm).
This problem requires careful thought.
It is interesting that the terminal speed can be found
with so little information about the metallic frame.
-cm).
This problem requires careful thought.
It is interesting that the terminal speed can be found
with so little information about the metallic frame.
Jess H. Brewer
2005-02-26

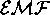 around the loop
as it enters the field?
around the loop
as it enters the field?
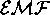 around the loop
around the loop
as a function of time, from the time it begins to enter the field
until it is entirely in the field.
around the loop
around the loop
as a function of time, from the time it begins to enter the field
until it is entirely in the field.

