THE UNIVERSITY OF BRITISH COLUMBIA
 
Physics 210 Assignment # 6:
 
FITTING
 
Tue. 19 Oct. 2010 - finish by Tue. 26 Oct.

In Assignments 4 and 5 you plotted points from the data file data.db (or its reformatted equivalent) with asymmetric uncertainties, using several different plotting applications. Some were far clumsier than others for this purpose, and in several cases I was unable to turn off the misleading little crossbars on the "error bars".¹ Now that we can get something on a graph, it's time to see which of these applications works best for comparing the data with a theoretical model. This is known as "fitting".

In any fitting model the theory has parameters whose values we optimize to obtain the best fit. Depending upon the complexity of the model and the data, there are many strategies for varying the parameters to find their best values in the shortest time.

There are also several possible criteria for defining "best", and we must choose one before we can even begin to fit. Probably the most powerful methods involve Bayesian inference,² in which one asks different kinds of questions from those one asks in more traditional methods involving frequency-based probability theory, which we will use in this course.³ Depending upon whether we have nonuniform "error bars" or not, we should use either $\chi^2$ ("chi squared") minimization (also known as "weighted least squares" fits) or "unweighted least squares" fits. The latter ignore uncertainties and merely seek to produce the smallest possible sum of the squares of the differences between experimental and theoretical values of the dependent variable:

$$\hbox{\rm Minimize ~ } \sum_{i=1}^N \left[Y(x_i,\Vec{p}) - y_i\right]^2$$ (1)

where the data consist of N ordered pairs ("points") (x_i,y_i) and $Y(x,\Vec{p})$ is the theoretical function of x and the n parameters $\Vec{p} \equiv \{p_1,p_2,\cdots,p_n\}$. Chi squared minimization is better:

$$\hbox{\rm Minimize ~ } \chi^2 \equiv \sum_{i=1}^N {\left[Y(x_i,\Vec{p}) - y_i\right]^2 \over \delta y_i^2}$$ (2)

where $\delta y_i$ is the uncertainty in y_i.

Note that it is generally assumed that only the dependent variable (generally "y") has uncertainties, and furthermore that those uncertainties are symmetric. This is rarely the case, as I have emphasized; I think people just give up too easily on "getting it right". My Java applet muview will of course handle asymmetric uncertainties, but none of the others will do this without a lot of "data massaging". To keep this Assignment from growing too complicated, you can use muview on the original file ~phys210/HW/a04/data.db (recall Assignment 4) but for the other applications we will just ignore any uncertainties in x_i and "symmetrize" the uncertainties in y_i as shown in the file ~phys210/HW/a06/dbf.dat and below:

1	-20	-1.9	0.2
1	-12	-1.2	0.2
1	-10	-0.95	0.075
2	-1	-0.05	0.05
3	5	0.55	0.075
3	7.5	0.8	0.175
3	10.5	1.1	0.1
3	15	1.6	0.1

where, as usual, the first column is the dataset number and the second column contains x_i values, but the third and fourth columns contain y_i and its uncertainty $\delta y_i$, respectively.

As usual, create your /home2/phys210/<you>/a06/ directory and the subdirectories muview/, gnuplot/, extrema/, matlab/, octave/ and python/, where you should store any files used to do the fitting, along with the plotted results, using the respective applications.

With each application, learn how to fit the data in data.db or dbf.dat and plot them along with the best fit line on a simple graph in a plotfit.pdf file, stored with the other files for that application, including a plain text file ANSWER.txt giving any comments plus the results of the fit [a description of the theoretical function $Y(x,\Vec{p})$, the best-fit values of its parameters p_j, the uncertainties $\delta p_j$ in the parameters p_j and the quality of the fit in $\chi^2$ per degree of freedom].

In real life you will want to fit with much more sophisticated functions $Y(x,\Vec{p})$, but here the emphasis is on procedure; moreover, the data in data.db and dbf.dat make a pretty straight line (as you may have noticed); so just fit to a first-order polynomial (i.e. a straight line), $Y(x,\Vec{p}) = p_0 + p_1 x$, using $\chi^2$ minimization.

Now, in python you can probably find any number of "canned" fitting packages just like those for the other applications; but python is a full-blown programming language in its own right, so we are going to tackle a real computational exercise in python, namely a simple one-step numerical calculation of the best (minimum $\chi^2$) fit to a straight line:

Y(x) = p₀ + p₁ x (3)

The first step you have already done: tell python to read from the dbf.dat file the number N of data points (x_i, y_i) and the uncertainties $\delta y_i$. Then we calculate the best values of p₀ and p₁ along with the resulting minimum value of $\chi^2$, using the following algorithm:

Expand Eq. (2) in terms of Eq. (3):

$$\begin{eqnarray*} \chi^2 &\equiv& \sum_{i=1}^N {\left[Y(x_i,\Vec{p}) - y_i\ri . . . . . . y_i - 2 p_1 \sum_{i=1}^N w_i x_i y_i + \sum_{i=1}^N w_i y_i^2 \end{eqnarray*}$$

where $w_i \equiv 1/\delta y_i^2$ can be thought of as a "weighting factor" for each data point. Note that $\chi^2$ can now be expressed as a function of two variables (p₀ and p₁) and a bunch of constants calculated from the data:

$$\chi^2 = p_0^2 S_0 + 2 p_0 p_1 S_x + p_1^2 S_{xx} - 2 p_0 S_y - 2 p_1 S_{xy} + S_{yy}$$ (4)

where the meanings of S₀, S_x, S_y, S_xx, S_xy and S_yy should be clear from the above.

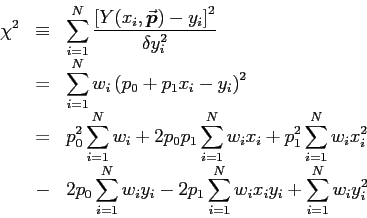
Our job is now to minimize that function with respect to p₀ and p₁ simultaneously. You know that a function has an extremum (maximum or minimum) where its derivative is zero. In this case we want both partial derivatives to be zero: $\partial \chi^2/\partial p_0 = 0$ and $\partial \chi^2/\partial p_1 = 0$. These requirements give two equations in two unknowns:

which you can easily solve for the values of p₁ and p₀ that give the minimum $\chi^2$:

$$p_1 = { S_0 S_{xy} - S_x S_y \over S_0 S_{xx} - S_x^2 } \quad \hbox{\rm and} \quad p_0 = { S_0 S_{xy} - S_x S_y \over S_0 S_{xx} - S_x^2 } \; .$$ (6)

This is pretty neat, and can (with considerable effort) be generalized to higher-order polynomial fits, but it lacks a vitally important feature: it does not yet tell you the uncertainty in your best-fit values for p₀ and p₁. These can be estimated by taking second derivatives and using the operational definition of one standard deviation in each parameter - namely, the displacement that causes $\chi^2$ to increase by 1. But let's leave that for later.

Don't forget to have your python program report the best fit and plot up the line through the points.