- . . . )1
-
If you go to
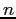 much larger than 10, it might be wise to plot
much larger than 10, it might be wise to plot
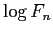 vs.
vs. 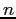 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . WikipediA2
-
You can Google them, or go directly to
http://en.wikipedia.org/wiki/Pauli_matrices
or http://mathworld.wolfram.com/PauliMatrices.html
to get a nice compact introduction to their mathematical properties.
Be sure you understand what "Hermitian" and "unitary" mean.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . particle.3
-
Actually, the Pauli matrices can be used to describe
the quantum mechanics of any two-state system,
which makes them useful not only in elementary particle physics
but also in a wide variety of quantum computing topics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . matrices.4
-
I don't find MatLab to be as great as it claims,
since I have not found a compact, elegant way to express
the three Pauli matrices
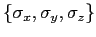 as a vector
as a vector
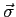 of matrices in MatLab,
even though that is a "natural" description in Physics.
This is possible with python; Google
NumPy for Matlab Users.
of matrices in MatLab,
even though that is a "natural" description in Physics.
This is possible with python; Google
NumPy for Matlab Users.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
thoroughly.5
- You'll thank me later!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . respectively.6
-
Thus
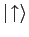 and
and
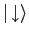 are the eigenvectors of
are the eigenvectors of 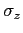 :
operating on them with
:
operating on them with 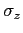 is the same as
multiplying them by a number which is their eigenvalue
with respect to
is the same as
multiplying them by a number which is their eigenvalue
with respect to 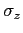 .
In the language of spin orientation,
the eigenvalue is the projection of the particle's spin
along the
.
In the language of spin orientation,
the eigenvalue is the projection of the particle's spin
along the 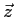 direction).
This follows from the fact that
direction).
This follows from the fact that 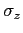 is diagonal.
is diagonal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . vectors,7
-
Such an interaction is known as a contact interaction
or a hyperfine interaction or a
Heisenberg spin-spin interaction.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . diagonal.8
-
If you need help with this, just ask!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . . 9
-
Actually there are
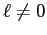 states mixed into the
"
states mixed into the
"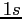 " state of a hydrogen atom if the two spins
are parallel; but this is a very small effect.
" state of a hydrogen atom if the two spins
are parallel; but this is a very small effect.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.