- . . . numerically?1
-
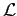 and
and 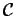 will, of course, vary
from one kind of transmission line to another, but
their product is a universal constant -
check, for example, the cable in Exercise 7.13 on p. 319 -
provided the space between the conductors is a vacuum.
In the theory of transmission lines, this product is
related to the speed at which a pulse propagates down the line
(
will, of course, vary
from one kind of transmission line to another, but
their product is a universal constant -
check, for example, the cable in Exercise 7.13 on p. 319 -
provided the space between the conductors is a vacuum.
In the theory of transmission lines, this product is
related to the speed at which a pulse propagates down the line
(
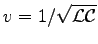 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . speed?2
-
Hint: see Exercise 4.6 on p. 183; by what factor does
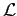 change when an inductor is immersed in linear material
of permeability
change when an inductor is immersed in linear material
of permeability 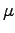 ?
?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ).
3
-
Note: this is not an additional force, but rather
an alternative way of calculating the same force -
in (b) we got it from the force law, and in (d) we got it
from conservation of momentum.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.