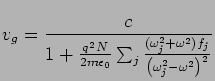
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
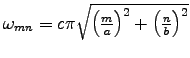 ,
the same as for TE modes.
,
the same as for TE modes.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
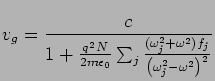
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
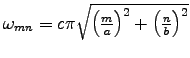 ,
the same as for TE modes.
,
the same as for TE modes.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .