. . . band?¹

You might also want to calculate the intensity of your cell phone's transmission signal at a distance of 10 cm (i.e. in your brain while you hold it to your ear). This is a topic upon which a great deal has been written. just Google it! But it's not part of this assignment.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . dipole.²

You should get $R = 3\times10^5 (b/\lambda)^4 \; \Omega$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

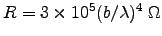. . . used.³

Relativistic electrons radiate furiously; this is known as Bremsstrahlung (German for "braking radiation", doh!) and is an important mechanism for energy loss of high energy electrons.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . thermal⁴

This thermal velocity corresponds to about 330 K, not far above room temperature, and so appears realistic. In point of fact, the conduction electrons in a good metal have velocities on the order of 10^-3c, thanks to the Pauli exclusion principle. However, their quantum mechanical wavefunctions are extended over distances large compared to 30 Å, and this classical picture of an accelerated point charge has to be reformulated with a quantum version. The present approximation is a reasonable compromise.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.