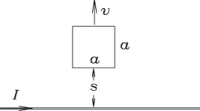
- Find the magnetic field due to the current carrying wire.
ANSWER: You've calculated this many times from AMPÈRE'S LAW.
The field due to the wire is coming straight out of the page
(which we'll call the
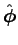 direction) normal to the
plane of the loop and drops off inversely with r,
the distance away from the wire:
direction) normal to the
plane of the loop and drops off inversely with r,
the distance away from the wire:
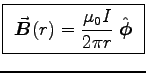 .
.
- Find the flux of
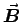 through the loop.
ANSWER: The flux
through the loop.
ANSWER: The flux 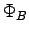 , like
, like 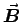 , is "up" through the loop.
For a given value of s, the flux through the loop is
, is "up" through the loop.
For a given value of s, the flux through the loop is
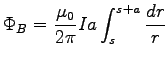 or
or
![\fbox{ ${\displaystyle
\Phi_B = {\mu_0 \over 2\pi} I a \ln
\left[ s+ a \over s \right] }$\ }](img11.gif) .
.
- If the loop is pulled directly away from the wire
(upwards in the diagram) at speed v, what is the emf generated?
ANSWER: Since B drops off as 1/r, the magnitude of the flux
through the loop will decrease as we pull it away from the wire.
Since
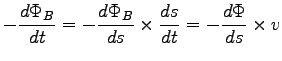 ,
FARADAY'S LAW gives
,
FARADAY'S LAW gives
![\begin{displaymath}{\cal E} = - {\mu_0 \over 2\pi} I
{a s \over s+a} \left[
{1 \over s} - {(s+a) \over s} \right] v
\end{displaymath}](img13.gif)
or![\fbox{ ${\displaystyle {\cal E} = - {\mu_0 \over 2\pi} I
{a s \over s+a} \left[ {1 \over s+a} - {1 \over s} \right] v }$\ }](img14.gif) .
.
- Does the induced current flow clockwise or counter-clockwise
in the loop?
ANSWER: By LENZ'S LAW, the induced emf
around the loop will cause a current to flow that produces its own
field in a direction that counteracts the change in flux - in this
case, to reestablish the decreasing flux "up" through the loop;
that means the current will flow around the loop
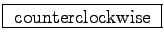 (as viewed).
(as viewed).
- What is the induced current in the loop if the loop is pulled
directly to the right, instead of upwards?
ANSWER: As long as the wire is really semi-infinite, nothing changes
(at least not
 ) and so there is no emf and
) and so there is no emf and
 .
.
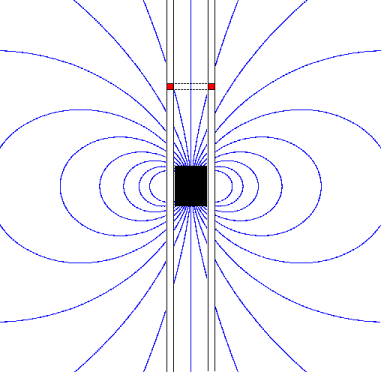
work out the analogue of the Lorentz force on a magnetic monopole moving at velocity
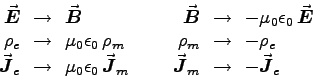
(see section 7.3.4 on p. 327). In this spirit, the LORENTZ FORCE
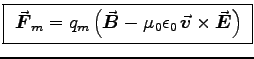 .
.
(If you like you can substitute 1/c2 for
What current is induced in the loop?
ANSWER: We mean "normal" (electrical) current, of course. Such current is driven by a "normal" (electrical) emf,
This makes a nice distinctive signal and tells one the magnitude of the detected monopole as well. Note that the size of the loop doesn't matter; monopole detectors can therefore employ lots and lots of very small loops that don't pick up much noise from randomly fluctuating ordinary magnetic fields.
There's no "correct answer" to this one!