ANSWER:
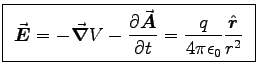 .
.
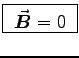 . These are the
. These are the 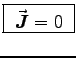 and
and
- Find the
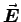 and
and 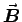 fields corresponding to
a stationary point charge q situated at the origin.
ANSWER: This is a freebie.
fields corresponding to
a stationary point charge q situated at the origin.
ANSWER: This is a freebie.
- State the charge and current distributions of this situation.
ANSWER: See above.
- What are the electric and magnetic potentials?
ANSWER:
We have learned to use
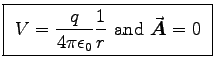 .
Those potentials are certainly not wrong, but they
don't look like the ones in Problem 10.3!
.
Those potentials are certainly not wrong, but they
don't look like the ones in Problem 10.3!
- Is there any relation between this situation
and that described in Problem 10.3?
ANSWER:
Well, obviously, since they give the same fields, they describe
exactly the same physics! This is a vivid illustration
of GAUGE INVARIANCE: an infinite variety of choices for
V and
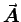 will all give the same
will all give the same 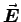 and
and 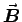 as long as they differ only by adding the gradient of some scalar
function to
as long as they differ only by adding the gradient of some scalar
function to 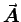 while subtracting the time derivative of the
same function from V.
while subtracting the time derivative of the
same function from V.
to transform the potentials in Problem 10.3, and comment on the result. ANSWER:
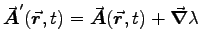 and
and
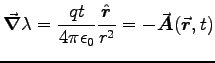 so
so
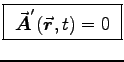 as in Problem 2. Meanwhile
as in Problem 2. Meanwhile
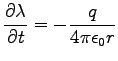 so
so
- In Problem 10.3 above,
are the potentials in the Coulomb gauge, the Lorentz gauge,
both, or neither?
ANSWER:
With
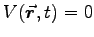 we have
we have
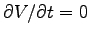 while
while
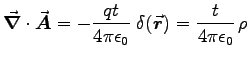 .
This is neither zero (Coublob gauge) nor
.
This is neither zero (Coublob gauge) nor 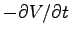 (Lorentz gauge), so the answer is
(Lorentz gauge), so the answer is
 .
.
- In Problem 2 above, are the potentials in the Coulomb gauge,
the Lorentz gauge, both, or neither?
ANSWER:
In this case V is constant in time, so again
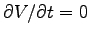 ;
meanwhile, if
;
meanwhile, if 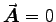 then
then
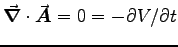 ,
so the answer in this case is
,
so the answer in this case is 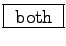 .
It's important to note that "being in" one gauge does not
preclude "being in" another!
.
It's important to note that "being in" one gauge does not
preclude "being in" another!
- In what units would we then measure velocities, momenta,
masses, forces and accelerations?
ANSWER:
Velocities are of course
 (
(
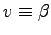 ).
Momenta are part of the same 4-vector as energies, and thus
differ from them only by factors of c=1
(e.g. for massless particles E = pc),
so momenta are also measured in
).
Momenta are part of the same 4-vector as energies, and thus
differ from them only by factors of c=1
(e.g. for massless particles E = pc),
so momenta are also measured in
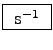 .
Masses are also measured in
.
Masses are also measured in
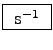 , since E = mc2.
Forces have the same units as the time rates of change of momenta,
namely
, since E = mc2.
Forces have the same units as the time rates of change of momenta,
namely
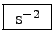 .
Accelerations are the time rate of change of velocities
or forces divided by masses; either way, they are measured in
.
Accelerations are the time rate of change of velocities
or forces divided by masses; either way, they are measured in
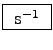 .
.
- Suppose we set the Coulomb force constant
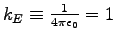 as well. In what units would we then measure charge, electric field,
magnetic field, and potentials V and
as well. In what units would we then measure charge, electric field,
magnetic field, and potentials V and 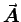 ?
ANSWER:
COULOMB'S FORCE LAW is now written
?
ANSWER:
COULOMB'S FORCE LAW is now written
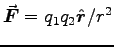 ,
so [charge]2 = [force] x [distance]2 so
Charge is
,
so [charge]2 = [force] x [distance]2 so
Charge is
 .
Electric field is force per unit charge, so it now has
the same units as force, namely
.
Electric field is force per unit charge, so it now has
the same units as force, namely
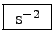 .
Alternatively, E2 is proportional to energy per unit volume.
Volume is in s3, so E2 is in s-4.
Thus again E is in s-2.
Magnetic field is in
.
Alternatively, E2 is proportional to energy per unit volume.
Volume is in s3, so E2 is in s-4.
Thus again E is in s-2.
Magnetic field is in
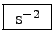 the same as
the same as 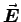 ,
because B2 is also proportional to energy per unit volume.1 V is
,
because B2 is also proportional to energy per unit volume.1 V is
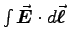 and
and 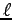 is in seconds,
since velocities are unitless; so V is in
is in seconds,
since velocities are unitless; so V is in
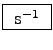 .
(This can also be deduced from U = q V.)
.
(This can also be deduced from U = q V.)
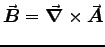 so
so 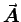 has one less s in its denominator:
it is measured in
has one less s in its denominator:
it is measured in
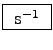 just like V.
(This should not be surprising.)
just like V.
(This should not be surprising.)
- Write out Maxwell's equations in this system of units.
(Hint: We must have
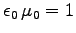 .)2ANSWER:
We have set
.)2ANSWER:
We have set
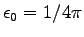 so we must set
so we must set 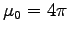 to ensure c=1. Then COULOMB'S LAW reads
to ensure c=1. Then COULOMB'S LAW reads
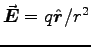 which, integrated over a sphere
centred on the charge, gives
which, integrated over a sphere
centred on the charge, gives
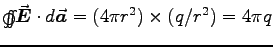 , so GAUSS' LAW has
a
, so GAUSS' LAW has
a 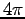 where the
where the 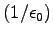 used to be, just as expected.
By the same token we expect to replace
used to be, just as expected.
By the same token we expect to replace 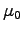 by
by 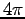 in the AMPÈRE/MAXWELL LAW; so Maxwell's equations
become just
in the AMPÈRE/MAXWELL LAW; so Maxwell's equations
become just
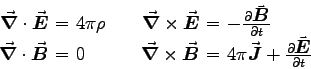
where both sides of each equation are measured in units of s-3. These are of course the "microscopic" equations; if we want to use the "macroscopic average" fields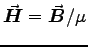 and
and
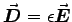 ,
we must include a dimensionless permittivity
,
we must include a dimensionless permittivity
 (where
(where 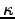 is the dielectric constant)
and dimensionless permeability
is the dielectric constant)
and dimensionless permeability
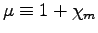 (where
(where 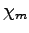 is the magnetic susceptibility).
is the magnetic susceptibility).
That was pretty simple. But before you get too enthusiastic, you might want to make a quantitative calculation of your own weight or the electron's charge in these units. For the former I get something like 1058 s-2. (I wouldn't want to have to paint the dials on bathroom scales if the world embraced these particular "natural units"!)3One can also set Newton's universal gravitational constant G=1 to define PLANCK UNITS, but I don't understand how that works. We already have everything covered, as far as I can see.