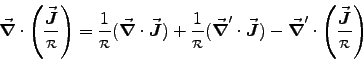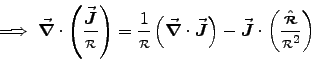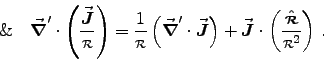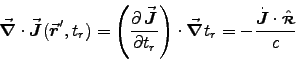ANSWER: Following the hint, we first show
where
and the (hopefully by now familiar) results
Adding together Eqs. (6) and (7) gives Eq. (3).
Next, noting that
Derivatives of
because, for a given
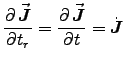 ,
and
,
and
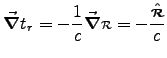 .
.
However,
because
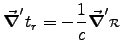
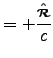 .
.
Finally we use this to calculate the divergence of
![\begin{eqnarray*}
\Div{A} &=& {\muz\over4\pi}\VolInt \left[
{1\over\rr}\left( . . .
. . . ime\cdot\left(\Vec{J}\over\rr\right) \right]
d\tau^\prime \; .
\end{eqnarray*}](img28.gif)
The DIVERGENCE THEOREM tells us that
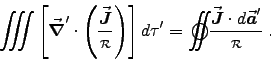
Now, if the closed surface encloses all the charges and currents in the source volume,
or
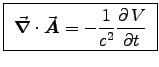 .
.
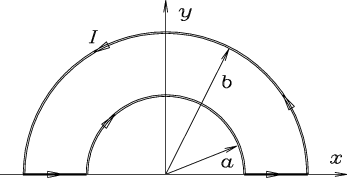
- Calculate the retarded vector potential
 at the center.
ANSWER:
Choose the origin at the same place as the field point: the centre.
Thus
at the center.
ANSWER:
Choose the origin at the same place as the field point: the centre.
Thus 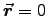 and
and
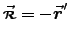 .
The source region is uncharged, so V = 0.
.
The source region is uncharged, so V = 0.
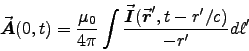
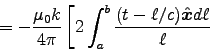
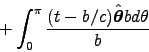
![\begin{displaymath}
- \left. \int_0^\pi {(t-a/c) \Hat{\theta} a d\theta \over a} \right]
\end{displaymath}](img40.gif)
where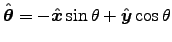 .
Now, by symmetry there is as much current going "up" as "down"
at the same
.
Now, by symmetry there is as much current going "up" as "down"
at the same  and tr, so the
and tr, so the  components cancel.
This leaves
components cancel.
This leaves
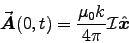
where

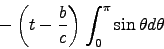
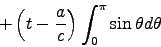
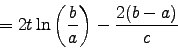
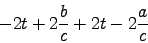
or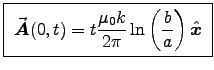 .
.
- Find the electric field at the center.
ANSWER: Since V=0 we have just
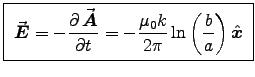 .
.
- Why does this (neutral) wire produce an electric field?
ANSWER:
Because the vector potential is changing with time, "Doh!"
I think this is meant as a retroactive hint
in case you got hung up on the preceding question.
- Why can't you determine the magnetic field
from this expression for
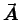 ?
?
ANSWER: Finding
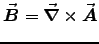 requires knowledge of the dependence
of
requires knowledge of the dependence
of 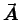 on
on 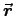 ; but we have calculated
; but we have calculated 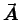 only
at one point in space! If you want a differentiable
only
at one point in space! If you want a differentiable
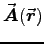 you will have a far more difficult calculation to perform.
you will have a far more difficult calculation to perform.
![\begin{displaymath}
V(\Vec{r},t) = {q\over4\pi\epsz}
\left[c \over \rr c - \Vec{\rr}\cdot\Vec{v}\right]_{\rm ret}
\end{displaymath}](img56.gif)
![\begin{displaymath}
\Vec{A}(\Vec{r},t) = V(\Vec{r},t) \left[\Vec{v}\over c^2\right]_{\rm ret}
\end{displaymath}](img57.gif)
where
For a point on the z axis,
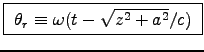 .
Then
.
Then
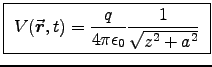 and
and
![\fbox{ ${\displaystyle
\Vec{A}(\Vec{r},t) = {\muz\over4\pi}
{a\omega q \over\sqrt{z^2 + a^2}} \left[-\Hat{x}\sin\theta_r
+ \Hat{y}\cos\theta_r\right]
}$\ }](img76.gif) .
.
- Calculate the electric field a distance d from the string,
using Eq. (10.68):
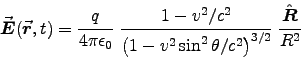
where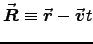 .
.
ANSWER: Suppose the field point is a perpendicular distance s from the string; measure z from the nearest point on the string, as shown in the diagram. Equation (10.68), in which we do not need to evaluate anything at a retarded time, gives the contribution to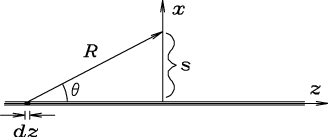
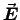 from a single charge q. We need to superimpose
such contributions from all charge elements
from a single charge q. We need to superimpose
such contributions from all charge elements
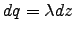 at positions
at positions
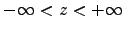 down the string:
for each of these we use
down the string:
for each of these we use
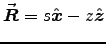 :
:
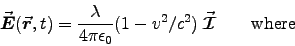
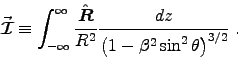
For each element dz at z there is an equal element dz at -z; thus the "horizontal" components cancel, leaving only the x component of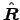 , namely
, namely
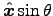 .
Meanwhile, since
.
Meanwhile, since
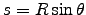 ,
,
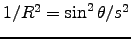 ; and since
; and since
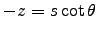 ,
,
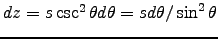 .
So
.
So
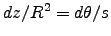 and
and
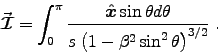
Let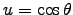 so that
so that
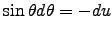 and
and
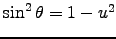 :
:
![\begin{displaymath}
\Vec{\cal I} = {\Hat{x}\over s} \int_{-1}^1 {du
\over \left( 1 - \beta^2 [1-u^2] \right)^{3/2} }
\end{displaymath}](img97.gif)
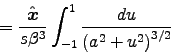
![\begin{displaymath}
= {\Hat{x}\over s\beta^3}
\left[u \over a^2 \sqrt{a^2 + u^2}\right]_{-1}^1
\end{displaymath}](img99.gif)
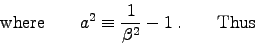
![\begin{displaymath}
\Vec{\cal I} = {\Hat{x}\over s\beta^3}\left[2 \over
\left({1\over\beta^2} - 1\right)\sqrt{{1\over\beta^2} - 1 + 1}\right]
\end{displaymath}](img101.gif)
![\begin{displaymath}
= {\Hat{x}\over s}\left[2 \over 1 - \beta^2 \right] \, ,
\qquad \hbox{\rm so}
\end{displaymath}](img102.gif)
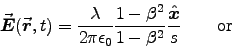
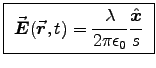
just as for a line charge at rest! - Find the magnetic field of this string, using Eq. (10.69):
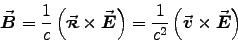
where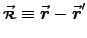 .
ANSWER:
Well,
.
ANSWER:
Well,
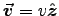 and
and
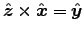 ,
so this is trivial:1
,
so this is trivial:1
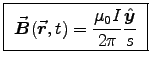
where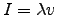 .
(Again, the same result as for a steady current in magnetostatics.)
.
(Again, the same result as for a steady current in magnetostatics.)