ANSWER:
For a simple resistor R driven by a power supply that moves
charge back and forth in an oscillation
![]() ,
we have a current
,
we have a current
![]() and a power
and a power
![]() which averages to
which averages to
![]() . Thus we can
associate
. Thus we can
associate
![]() .
Plugging in the average power radiated by the electric dipole,
.
Plugging in the average power radiated by the electric dipole,
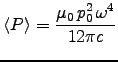 , with p0 = q0 d, we get
, with p0 = q0 d, we get
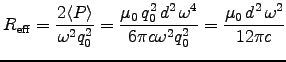 . Since
. Since
![]() , we can substitute
, we can substitute
![]() to get
to get
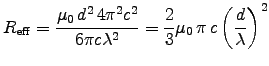 . The coefficient
. The coefficient
![]() N-A-2m-s-1,
whose units are equivalent to W/A-2
or
N-A-2m-s-1,
whose units are equivalent to W/A-2
or ![]() , leaving
, leaving
![\fbox{ ${\displaystyle
R_{\rm eff} = [789 \; \Omega] \times \left(d \over \lambda\right)^2
}$\ }](img15.gif) .
.
For 900 or 1900 MHz, we have
![]() cm or 15.8 cm,
respectively,2
giving radiation resistances of
cm or 15.8 cm,
respectively,2
giving radiation resistances of
![]() or
or
![]() , respectively.
Neither is a huge resistance, but both are certainly larger than
that of the wires in your cell phone.
The power is thus used quite efficiently.
(Very little goes into useless heat; almost all is transmitted!)
This is even more true of the higher frequency band:
whatever transmission intensity is required,
it can be realized with a smaller I.
, respectively.
Neither is a huge resistance, but both are certainly larger than
that of the wires in your cell phone.
The power is thus used quite efficiently.
(Very little goes into useless heat; almost all is transmitted!)
This is even more true of the higher frequency band:
whatever transmission intensity is required,
it can be realized with a smaller I.
ANSWER:
For the magnetic dipole,
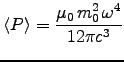 where
where
![]() . Again setting this equal to
. Again setting this equal to
![]() , we get
, we get
![]()
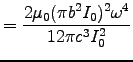
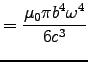 .
Again substituting
.
Again substituting
![]() for
for ![]() , we get
, we get
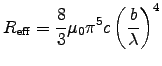 . The coefficient
. The coefficient
![]() , so
, so
![\fbox{ ${\displaystyle R_{\rm eff} =
[3.074\times10^5 \; \Omega] \times \left(b \over \lambda\right)^4
}$\ }](img33.gif) .
.
In this case, for a given frequency, the radiation resistance
increases as the square of the area of the loop.
For
![]() cm or 15.8 cm, a 2.5 cm radius loop
would have
cm or 15.8 cm, a 2.5 cm radius loop
would have
![]() or
or
![]() ,
respectively. Thus the magnetic dipole antenna is similar
to the electric dipole antenna at this size and frequency,
but is much more strongly size- and frequency-dependent.
,
respectively. Thus the magnetic dipole antenna is similar
to the electric dipole antenna at this size and frequency,
but is much more strongly size- and frequency-dependent.
- Suppose an electron decelerates at a constant rate a
from some initial velocity v0 down to zero.
What fraction of its initial kinetic energy is lost to EM radiation?
(The rest is absorbed by whatever mechanism
keeps the acceleration constant.) Assume
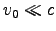 (nonrelativistic case) so that the Larmor formula can be used.4
(nonrelativistic case) so that the Larmor formula can be used.4
ANSWER: The LARMOR FORMULA says
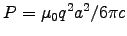 .
This is expended for a time t = v0/a, giving a total
radiated energy
.
This is expended for a time t = v0/a, giving a total
radiated energy
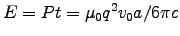 .
The initial kinetic energy
.
The initial kinetic energy
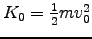 .
Thus the fraction lost to EM radiation is
.
Thus the fraction lost to EM radiation is
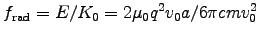 or
or
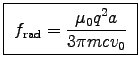 .
.
- To get a sense of the numbers involved,
suppose the initial velocity is thermal5 (around 105 m/s)
and the distance over which the electron decelerates to rest is 30 Å.
What can you conclude about radiation losses for electrons
in an ordinary conductor?
ANSWER: Using v02 = 2 a d with v0 = 105 m/s and d = 3 x 10-9 m, we have a = v02/2d = 1010/6 x 10-9 = 1.67 x 1018 m/s2. With q = -1.602 x 10-19 C and m = 0.911 x 10-30 kg, we get
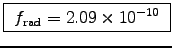 . (Not much!)
The true picture is much stranger, of course; electrons are not
localized point charges following classical trajectories,
they are described by extended wavefunctions and do not radiate
at all in things like atoms (luckily!).
. (Not much!)
The true picture is much stranger, of course; electrons are not
localized point charges following classical trajectories,
they are described by extended wavefunctions and do not radiate
at all in things like atoms (luckily!).
- Show that the linear charge density is
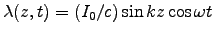 ,
(i.e. the charge density is maximum at the times when
the current is zero.)
,
(i.e. the charge density is maximum at the times when
the current is zero.)
ANSWER: For a half-wave antenna
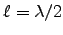 and
and 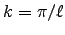 .
Charge conservation requires
.
Charge conservation requires
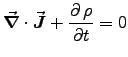 .
For a 1-dimensional wire with a current I(z,t)
flowing in the
.
For a 1-dimensional wire with a current I(z,t)
flowing in the  direction, the same logic demands
direction, the same logic demands
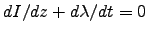 where
where
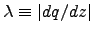 .
Thus
.
Thus
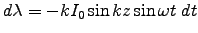 .
Integrating,
.
Integrating,

where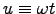 and
and
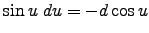 , giving
, giving
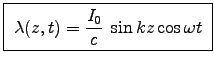 .
.
Note that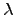 is also maximum at the places where
the current is zero.
is also maximum at the places where
the current is zero.
- If an FM radio station broadcasts at a frequency of 10 MHz
with a power of 10 kW from a half-wave antenna,
how long must the antenna be? What is the current?
ANSWER: The length is simple:
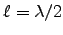 where
where
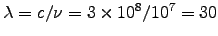 m. Thus
m. Thus
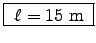 .
The current we can get from the power, using
.
The current we can get from the power, using
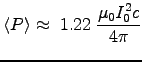 = 104 W. Thus
= 104 W. Thus
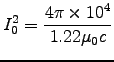 or
or
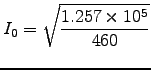 or
or
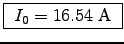 .
.