We can now put the second part of the procedure
[calculating the forces on a test charge
due to known FIELDS] into a very compact form
combining both the electric and the magnetic forces
into one equation.
If a particle with charge q and mass m moves
with velocity ![]() in the combination of
a uniform electric field
in the combination of
a uniform electric field ![]() and
a uniform magnetic field
and
a uniform magnetic field ![]() ,
the net force acting on the particle is the LORENTZ FORCE,
which can be written (in one set of units)
,
the net force acting on the particle is the LORENTZ FORCE,
which can be written (in one set of units)
If
![]() and
and ![]() is perpendicular to
is perpendicular to ![]() ,
the Lorentz force is perpendicular to both
,
the Lorentz force is perpendicular to both ![]() and the momentum
and the momentum
![]() .
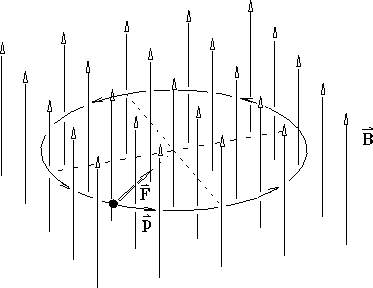
The force will deflect the momentum sideways,
changing its direction but not its magnitude.17.6
As
.
The force will deflect the momentum sideways,
changing its direction but not its magnitude.17.6
As ![]() changes direction,
changes direction, ![]() changes
with it to remain ever perpendicular to the velocity -
this is an automatic property of the cross product -
and eventually the orbit of the particle closes back
on itself to form a circle. In this way
the magnetic field produces UNIFORM CIRCULAR MOTION
with the plane of the circle perpendicular
to both
changes
with it to remain ever perpendicular to the velocity -
this is an automatic property of the cross product -
and eventually the orbit of the particle closes back
on itself to form a circle. In this way
the magnetic field produces UNIFORM CIRCULAR MOTION
with the plane of the circle perpendicular
to both ![]() and
and ![]() .
.
 |
Using Newton's SECOND LAW and a general knowledge of
circular motion, one can derive a formula for
the radius of the circle (r) in terms of the
momentum of the particle (p = mv), its charge (q)
and the magnitude of the magnetic field (B).
In "Gaussian units" (grams, centimeters, Gauss) the formula
reads17.7
It is also interesting to picture qualitatively what will happen
to the particle if an electric field ![]() is then applied parallel to
is then applied parallel to ![]() :
since
:
since ![]() accelerates the charge in the direction of
accelerates the charge in the direction of ![]() ,
which is also the direction of
,
which is also the direction of ![]() ,
and since
,
and since
![]() only produces a force when the particle moves
perpendicular to
only produces a force when the particle moves
perpendicular to ![]() ,
in effect the "perpendicular part of
the motion" is unchanged (circular motion) while the "parallel
part" is unrestricted acceleration. The path in space followed
by the particle will be a spiral with steadily increasing
"pitch":
,
in effect the "perpendicular part of
the motion" is unchanged (circular motion) while the "parallel
part" is unrestricted acceleration. The path in space followed
by the particle will be a spiral with steadily increasing
"pitch":