

Next: Momentum
Up: Inertia vs. Weight
Previous: Inertia vs. Weight
Is there any way to test Newton's conjecture that
"inertial mass" (the quantitative measure of an objects resistance
to acceleration by an applied force) is different from
"gravitational mass" (the factor determining the weight of said object)?
Certainly. But first we must make the proposition more explicit:
- Inertial mass
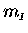 is an additive property of matter.
That is, two identical objects, when combined, will have twice the
inertial mass of either one by itself.5
is an additive property of matter.
That is, two identical objects, when combined, will have twice the
inertial mass of either one by itself.5
- When subjected to a given force
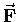 [a vector quantity, since it certainly has both magnitude and direction],
an object will be accelerated in the direction of
[a vector quantity, since it certainly has both magnitude and direction],
an object will be accelerated in the direction of
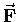 at a rate
at a rate
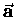 which is inversely proportional4
to its inertial mass
which is inversely proportional4
to its inertial mass
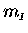 .
Mathematically,
.
Mathematically,
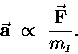 |
(1) |
- Gravitational mass
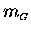 is also an additive property of matter.
is also an additive property of matter.
- The force of gravity
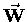 pulling an object "down"
toward the centre of the Earth (i.e. its weight)
is proportional to its gravitational mass
pulling an object "down"
toward the centre of the Earth (i.e. its weight)
is proportional to its gravitational mass
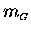 .
Let's write the constant
of proportionality "g" so that
.
Let's write the constant
of proportionality "g" so that
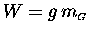 (where
(where
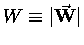 is the magnitude of the weight, which is usually all we need,
knowing as we do which way is "down") - or, in full vector notation,
is the magnitude of the weight, which is usually all we need,
knowing as we do which way is "down") - or, in full vector notation,
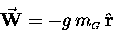 |
(2) |
(where
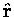 is the unit vector pointing
from the centre of the Earth to the object in question).
is the unit vector pointing
from the centre of the Earth to the object in question).
The combination of the last two postulates
is easy to check using a simple balance.
However, it is not so easy to separately
check these two propositions. See why?
Fortunately, we don't have to.
If we put together the two equations
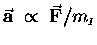 and
and
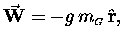 noting that, in the case of the force of gravity itself,
noting that, in the case of the force of gravity itself,
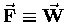 ,
we get
,
we get
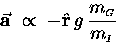 |
(3) |
- i.e. the acceleration due to gravity is in the
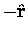 direction (towards the centre of the Earth), and is proportional to
the ratio of the gravitational mass to the inertial mass.
So... if the gravitational mass is proportional to
the inertial mass, then all objects should experience the same
acceleration when falling due to the force of gravity, at least
in the absence of any other forces like air friction.
Wait! Isn't this just what Galileo was always trying to tell us?
Yep. But was he right?
direction (towards the centre of the Earth), and is proportional to
the ratio of the gravitational mass to the inertial mass.
So... if the gravitational mass is proportional to
the inertial mass, then all objects should experience the same
acceleration when falling due to the force of gravity, at least
in the absence of any other forces like air friction.
Wait! Isn't this just what Galileo was always trying to tell us?
Yep. But was he right?
Clearly the answer hangs on the proportionality of
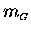 and
and
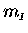 .
As we shall see, any nontrivial constant of proportionality
can be absorbed into the definition of the units of force;
thus instead of
.
As we shall see, any nontrivial constant of proportionality
can be absorbed into the definition of the units of force;
thus instead of
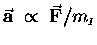 we can write
we can write
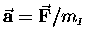 and the question becomes,
"Are inertial mass and gravitational mass the same thing?"
The experimental test is of course to actually drop a variety
of objects in an evacuated chamber where there truly is no air friction
(nor, we hope, any other more subtle types of friction)
and measure their accelerations as accurately as possible.
This was done by Eötvös to an advertised accuracy of
10-9 (one part per billion - often written 1 ppb)
who found satisfactory agreement with Galileo's "law."6
Henceforth I will therefore drop the G and I subscripts
on mass and assume there is only one kind, mass,
which I will write m.
and the question becomes,
"Are inertial mass and gravitational mass the same thing?"
The experimental test is of course to actually drop a variety
of objects in an evacuated chamber where there truly is no air friction
(nor, we hope, any other more subtle types of friction)
and measure their accelerations as accurately as possible.
This was done by Eötvös to an advertised accuracy of
10-9 (one part per billion - often written 1 ppb)
who found satisfactory agreement with Galileo's "law."6
Henceforth I will therefore drop the G and I subscripts
on mass and assume there is only one kind, mass,
which I will write m.


Next: Momentum
Up: Inertia vs. Weight
Previous: Inertia vs. Weight
Jess H. Brewer -
Last modified: Fri Nov 13 17:32:09 PST 2015
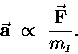
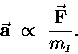
![]() and
and
![]() noting that, in the case of the force of gravity itself,
noting that, in the case of the force of gravity itself,
![]() ,
we get
,
we get
![]() and
and
![]() .
As we shall see, any nontrivial constant of proportionality
can be absorbed into the definition of the units of force;
thus instead of
.
As we shall see, any nontrivial constant of proportionality
can be absorbed into the definition of the units of force;
thus instead of
![]() we can write
we can write
![]() and the question becomes,
"Are inertial mass and gravitational mass the same thing?"
The experimental test is of course to actually drop a variety
of objects in an evacuated chamber where there truly is no air friction
(nor, we hope, any other more subtle types of friction)
and measure their accelerations as accurately as possible.
This was done by Eötvös to an advertised accuracy of
10-9 (one part per billion - often written 1 ppb)
who found satisfactory agreement with Galileo's "law."6
Henceforth I will therefore drop the G and I subscripts
on mass and assume there is only one kind, mass,
which I will write m.
and the question becomes,
"Are inertial mass and gravitational mass the same thing?"
The experimental test is of course to actually drop a variety
of objects in an evacuated chamber where there truly is no air friction
(nor, we hope, any other more subtle types of friction)
and measure their accelerations as accurately as possible.
This was done by Eötvös to an advertised accuracy of
10-9 (one part per billion - often written 1 ppb)
who found satisfactory agreement with Galileo's "law."6
Henceforth I will therefore drop the G and I subscripts
on mass and assume there is only one kind, mass,
which I will write m.