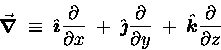

Next: GRADIENTS of Scalar Functions
Up: Vector Calculus
Previous: Functions of Several Variables
The foregoing description applies for any function of (x,y,z);
the concept of "taking partial derivatives" is independent
of what function we are taking the derivatives of.
It is therefore practical to learn to think of
as OPERATORS that can be applied to any function
(like F). Put the operator on the left of a function,
perform the operation and you get a partial derivative -
a new function of (x,y,z).
In general, such "operators" change one function into another.
Physics is loaded with operators like these.
The GRADIENT Operator
The GRADIENT operator is a vector operator,
written  and called "grad" or "del." It is defined
(in Cartesian coordinates x,y,z) as1
and called "grad" or "del." It is defined
(in Cartesian coordinates x,y,z) as1
and can be applied directly to any scalar function
of (x,y,z) - say,
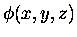 -- to turn it into a
vector function,
-- to turn it into a
vector function,
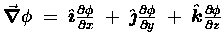 .
.
Jess H. Brewer -
Last modified: Wed Nov 18 12:22:08 PST 2015
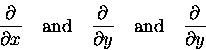
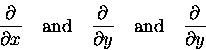
![]() and called "grad" or "del." It is defined
(in Cartesian coordinates x,y,z) as1
and called "grad" or "del." It is defined
(in Cartesian coordinates x,y,z) as1