BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

DIVERGENCE of a Vector Field

If we form the scalar ("dot") product of $\Grad{}$ with a vector function $\Vec{A}(x,y,z)$ we get a scalar result called the DIVERGENCE of $\Vec{A}$:

$$\hbox{\rm div} \Vec{A} \; \equiv \; \Div{A} \; \equiv \; . . . . . . y \over \partial y} \, + \, {\partial{A}_z \over \partial z}$$

This name is actually quite mnemonic: the DIVERGENCE of a vector field is a local measure of its "outgoingness" -- i.e. the extent to which there is more exiting an infinitesimal region of space than entering it. If the field is represented as "flux lines" of some indestructible "stuff" being emitted by "sources" and absorbed by "sinks," then a nonzero DIVERGENCE at some point means there must be a source or sink at that position. That is to say,

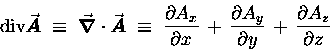
"What leaves a region is no longer in it."

For example, consider the divergence of the CURRENT DENSITY $\Vec{J}$, which describes the FLUX of a CONSERVED QUANTITY such as electric charge Q. (Mass, as in the current of a river, would do just as well.)

  

To make this as easy as possible, let's picture a cubical volume element $dV = dx \, dy \, dz$. In general, $\Vec{J}$ will (like any vector) have three components (J_x, J_y, J_z), each of which may be a function of position (x,y,z). If we take the lower left front corner of the cube to have coordinates (x,y,z) then the upper right back corner has coordinates $(x+dx, \, y+dy, \, z+dz)$. Let's concentrate first on J_z and how it depends on z.

It may not depend on z at all, of course. In this case, the amount of Q coming into the cube through the bottom surface (per unit time) will be the same as the amount of Q going out through the top surface and there will be no net gain or loss of Q in the volume - at least not due to J_z.

If J_z is bigger at the top, however, there will be a net loss of Q within the volume dV due to the "divergence" of J_z. Let's see how much: the difference between J_z(z) at the bottom and J_z(z+dz) at the top is, by definition, $dJ_z = \left(\partial J_z \over \partial z \right) dz$. The flux is over the same area at top and bottom, namely $dx \, dy$, so the total rate of loss of Q due to the z-dependence of J_z is given by

$$\dot{Q}_z \; = \; - dx \, dy \left(\partial J_z \over \part . . . . . . - \left(\partial J_z \over \partial z \right) dx \, dy \, dz$$

$$\mbox{\rm or} \quad \dot{Q} \; = \; - \left(\partial J_z \over \partial z \right) dV .$$

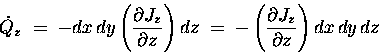
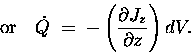
A perfectly analogous argument holds for the x-dependence if J_x and the y-dependence of J_y, giving a total rate of change of Q

$$\dot{Q} \; = \; - \left( {\partial J_x \over \partial x} \, . . . . . . y} \, + \, {\partial J_z \over \partial z} \right) \, dV$$

$$\mbox{\rm or} \quad \dot{Q} \; = \; - \Div{J} \; dV$$

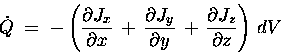
The total amount of Q in our volume element dV at a given instant is just $\rho \, dV$, of course, so the rate of change of the enclosed Q is just

$$\dot{Q} \; = \; \dot{\rho} \; dV$$

which means that we can write

$${\partial \rho \over \partial t} \, dV \; = \; - \Div{J} \, dV$$

or, just cancelling out the common factor dV on both sides of the equation,

$$\fbox{\hbox{$\displaystyle {\partial \rho \over \partial t} \; = \; - \Div{J} $}}$$

which is the compact and elegant "differential form" of the EQUATION OF CONTINUITY.

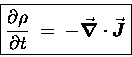
This equation tells us that the "Q sourciness" of each point in space is given by the degree to which flux "lines" of $\Vec{J}$ tend to radiate away from that point more than they converge toward that point - namely, the DIVERGENCE of $\Vec{J}$ at the point in question. This esoteric-looking mathematical expression is, remember, just a formal way of expressing our original dumb tautology!