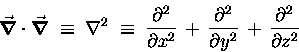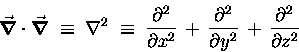

Next: GAUSS' LAW
Up: Vector Calculus
Previous: CURL of a Vector Field
If we form the scalar ("dot") product
of  with itself
we get a scalar second derivative operator
called the LAPLACIAN:
with itself
we get a scalar second derivative operator
called the LAPLACIAN:
What does the 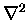 operator "mean?"
It is the three-dimensional generalization of the
one-dimensional CURVATURE operator d2/dx2.
Consider the familiar one-dimensional function h(x)
where h is the height of a hill at horizontal position x.
Then dh/dx is the slope of the hill and
d2h/dx2 is its curvature
(the rate of change of the slope with position).
This property appears in every form of the WAVE EQUATION.
In three dimensions, a nice visualization is harder
(there is no extra dimension "into which to curve")
but
operator "mean?"
It is the three-dimensional generalization of the
one-dimensional CURVATURE operator d2/dx2.
Consider the familiar one-dimensional function h(x)
where h is the height of a hill at horizontal position x.
Then dh/dx is the slope of the hill and
d2h/dx2 is its curvature
(the rate of change of the slope with position).
This property appears in every form of the WAVE EQUATION.
In three dimensions, a nice visualization is harder
(there is no extra dimension "into which to curve")
but
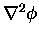 represents the equivalent property of
a scalar function
represents the equivalent property of
a scalar function
 .
.
Jess H. Brewer -
Last modified: Wed Nov 18 12:25:08 PST 2015