

Next: Weighing the Earth
Up: Celestial Mechanics
Previous: Kepler's Laws of Planetary Motion
By a process of logic that I will not attempt to describe,
Newton deduced that the force F between two objects with
masses m and M separated by a distance r
was given by
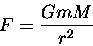 |
(10.3) |
where
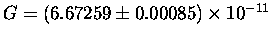 m
m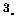 kg
kg
 s-2
is the Universal Gravitational Constant.
Actually, Newton didn't know the value of G;
he only postulated that it was universal -
i.e. that it was the same constant of proportionality
for every pair of masses in this universe.
The actual determination of the value of G
was first done by Cavendish
in an experiment to be described below.
s-2
is the Universal Gravitational Constant.
Actually, Newton didn't know the value of G;
he only postulated that it was universal -
i.e. that it was the same constant of proportionality
for every pair of masses in this universe.
The actual determination of the value of G
was first done by Cavendish
in an experiment to be described below.
We should also express this equation in vector form
to emphasize that the force on either mass acts in the
direction of the other mass:
if
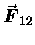 denotes
the force acting on mass m2
due to its gravitational attraction by mass m1 then
denotes
the force acting on mass m2
due to its gravitational attraction by mass m1 then
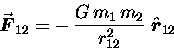 |
(10.4) |
where
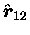 is a unit vector in the direction of
is a unit vector in the direction of
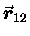 ,
the vector distance from m1 to m2,
and r12 is the scalar magnitude of
,
the vector distance from m1 to m2,
and r12 is the scalar magnitude of
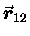 .
Note that the reaction force
.
Note that the reaction force
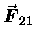 on m1 due to m2 is obtained by interchanging the labels
"1" and "2" which ensures that it is equal and opposite
because
on m1 due to m2 is obtained by interchanging the labels
"1" and "2" which ensures that it is equal and opposite
because
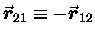 by definition.
by definition.


Next: Weighing the Earth
Up: Celestial Mechanics
Previous: Kepler's Laws of Planetary Motion
Jess H. Brewer -
Last modified: Sat Nov 14 12:27:25 PST 2015
![]() denotes
the force acting on mass m2
due to its gravitational attraction by mass m1 then
denotes
the force acting on mass m2
due to its gravitational attraction by mass m1 then