

Next: The Principles of Inertia and Superposition
Up: Weapons Research: Telescopes and Trajectories
Previous: Weapons Research: Telescopes and Trajectories
In terms of our newly-acquired left hemisphere skills,
if we use y to designate height [say, above sea level]
and t to designate time, then the upward velocity
vy [where the subscript tells us explicitly that this is the
upward velocity as opposed to the horizontal
velocity which would probably be written vx]6.9
is given by
where vy0 is the initial6.10
upward velocity
(i.e. the upward velocity at t=0), if any,6.11
and g is the downward6.12
acceleration of gravity,
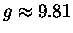 m/s2 on average
at the Earth's surface.6.13
Another way of writing the same equation is in terms of the
derivative of the velocity with respect to time,
m/s2 on average
at the Earth's surface.6.13
Another way of writing the same equation is in terms of the
derivative of the velocity with respect to time,
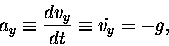 |
(6.2) |
where I have introduced yet another
notational convention used by Physicists:
a little dot above a symbol means the time derivative of
that symbol - i.e. the rate of change (per unit time) of the quantity
represented by that symbol.6.14
And since vy is itself the time derivative
of the height y [i.e.
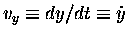 ],
if we like we can write the original equation as
],
if we like we can write the original equation as
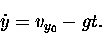 |
(6.3) |
All these notational gymnastics have several purposes,
one of which is to make you appreciate the simple clarity
of the declaration, "The vertical speed increases
by equal increments in equal times," as originally stated
by Galileo himself. But I also want you to see how Physicists
like to condense their notation until a very compact
equation "says it all."


Next: The Principles of Inertia and Superposition
Up: Weapons Research: Telescopes and Trajectories
Previous: Weapons Research: Telescopes and Trajectories
Jess H. Brewer -
Last modified: Fri Nov 13 17:05:58 PST 2015