

Next: The Scientific Method
Up: Weapons Research: Telescopes and Trajectories
Previous: The Principles of Inertia and Superposition
Applied to the case of trajectories
close to the Earth's surface,6.17
the equations governing constant horizontal velocity
superimposed upon constant downward acceleration
take the form
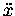 |
= |
0 |
(6.4) |
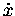 |
= |
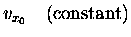 |
(6.5) |
| x |
= |
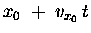 |
(6.6) |
 |
|
 |
(6.7) |
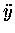 |
= |
- g |
(6.8) |
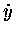 |
= |
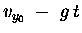 |
(6.9) |
| y |
= |
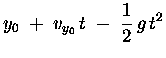 |
(6.10) |
where
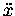 |
 |
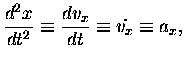 |
(6.11) |
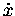 |
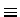 |
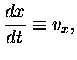 |
(6.12) |
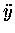 |
 |
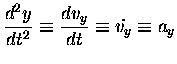 |
(6.13) |
 |
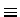 |
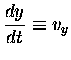 |
(6.14) |
Hold it! Before you bolt for the door, take a moment to
casually read through all these horrible-looking equations.
I have made them look long and hirsute on purpose,
for two reasons: first, because this way they are in their
most general form - i.e. we can be confident that
these equations will correctly describe any
trajectory problem, but for any actual problem
the equations will usually simplify;
and second, because this is a sort of practical joke -
if you look carefully you will see that the equations are
really pretty simple! All those "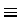 " symbols just
mean, "...another way of putting it, which amounts to
exactly the same thing, is...." That is, they just
indicate equivalent notations - or, in the language
of linguistics, synonyms. So the latter batch of equations
is just reminding you of the convention Physicists use for
writing time derivatives: "dot" and "double-dot" notation.
The first batch of equations tells you (in this notation)
everything there is to know about the motion:
the horizontal [x] motion is not under any acceleration
[
" symbols just
mean, "...another way of putting it, which amounts to
exactly the same thing, is...." That is, they just
indicate equivalent notations - or, in the language
of linguistics, synonyms. So the latter batch of equations
is just reminding you of the convention Physicists use for
writing time derivatives: "dot" and "double-dot" notation.
The first batch of equations tells you (in this notation)
everything there is to know about the motion:
the horizontal [x] motion is not under any acceleration
[
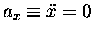 ]
so the horizontal velocity
[
]
so the horizontal velocity
[
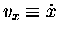 ]
is constant [
]
is constant [
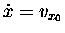 ]
and the distance travelled horizontally [x(t)] is just
increasing linearly with time t relative to its initial
value x0 - i.e.
x = x0 + vx0t.
The vertical motion differs only in that it includes a
constant downward acceleration [
]
and the distance travelled horizontally [x(t)] is just
increasing linearly with time t relative to its initial
value x0 - i.e.
x = x0 + vx0t.
The vertical motion differs only in that it includes a
constant downward acceleration [
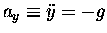 ]
which adds a term [-gt] to
]
which adds a term [-gt] to 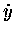 and another
familiar term [
and another
familiar term [
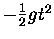 ]
to y(t).
Note that in every case the whole idea is to get the
quantity on the left-hand side [lhs] of the equation
equal to an explicit function of t on the
right-hand side [rhs].
]
to y(t).
Note that in every case the whole idea is to get the
quantity on the left-hand side [lhs] of the equation
equal to an explicit function of t on the
right-hand side [rhs].
Let's do a problem to illustrate how these equations work:
Suppose we fire a cannon horizontally
from the top of a 19.62 m high bluff,
imparting an initial velocity
vx0 = 10 m/s to the cannonball.
[By the definition of "horizontal,"
vy0 = 0.]
Where does the ball hit? [We neglect air friction and
assume level (horizontal) ground at the bottom of the bluff.]
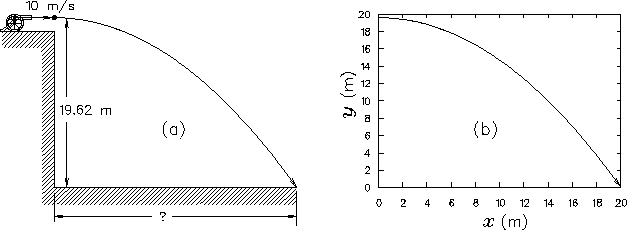
Figure:
(a) Sketch of a trajectory problem in which the initial height
[
y0 = 19.62 m] and the initial (horizontal) velocity
[
vx0 = 10 m/s] are given and we want to calculate
the horizontal distance [xf] at which the cannonball
hits the ground [yf = 0].
(b) Corresponding plot of y(x), the trajectory
followed by the cannonball.
 |
For simplicity we can take x=0 at the muzzle of the
cannon;6.18
similarly, we (naturally enough) take t=0 to be the instant
at which the ball leaves the muzzle of the cannon.
Our general equations now "reduce" to
a more particular set of equations for this specific example:
or, since
vx0 = 10 m/s and
y0 = 19.62 m,
We now have a choice between
working out the algebra in the first pair of equations or
working out the arithmetic in the second pair.
The former is preferable partly because we don't have to
"juggle units" while we work out the equations
(a clumsy process which is usually neglected, leading to
equations with numbers but no units, which in turn can lead
to considerable confusion) and because solving for xf
in terms of the two "parameters" y0 and vx0
[g is also a parameter, although we usually treat it
as if it were a constant of Nature] gives an "answer"
to any such problem with qualitatively
similar conditions. Here's the algebra:
which can be substituted for t in the second equation, giving
We are interested in the value of xf at the end of the trajectory
-- i.e. when yf = 0:
Now we "plug in"
y0 = 19.62 m,
vx0 = 10 m/s
and g = 9.81 m/s2, giving
And that's the answer: xf = 20 m. Simple, huh?


Next: The Scientific Method
Up: Weapons Research: Telescopes and Trajectories
Previous: The Principles of Inertia and Superposition
Jess H. Brewer -
Last modified: Fri Nov 13 17:06:41 PST 2015
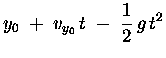
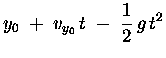
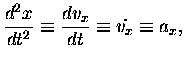
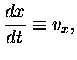
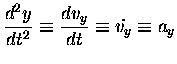
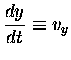

![\begin{displaymath}y = y_0 \; - \; {1\over2} \, g \, \left[ x \over v_{x_0} \right]^2 . \end{displaymath}](img36.gif)
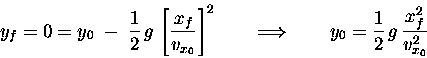
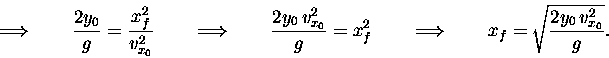
![\begin{displaymath}x_f = \sqrt{2 \times 19.62{\rm m} \times [10 {\rm m/s}]^2
\...
...ver 9.81 {\rm m/s}^2 }
= \sqrt{400 {\rm m}^2 } = 20 {\rm m}. \end{displaymath}](img39.gif)