BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

Algebra 1

A handy trick for introducing Algebra to young children (who have not yet learned that it is supposed to be too hard for them) is to phrase a typical Algebra problem in the following way: "I'm thinking of a number, and its name is `x' . . . so if 2x + 3 = 7, what is x?" (You may have to spend a little time explaining the notational conventions of equations and that 2x means 2 times x.) Most 7-year-olds can then solve this problem by inspection (my son and daughter both could!) but they may not be able to tell you how they solved it. This suggests either that early Arithmetic has already sown the seeds of algebraic manipulation conventions or that there is some understanding of such concepts "wired in" to our brains. We will never know how much of each is true, but certainly neither is entirely false!

What we learn in High School Algebra is to examine how we solve problems like this and to refine these techniques by adapting ourselves to a particular formalism and technology. Unfortunately our intuitive understanding is often trampled upon in the process - this happens when we are actively discouraged from treating the technology as a convenient representation for what we already understand, rather than a definition of correct procedure.

In Algebra we learn to "solve" equations. What does that mean? Usually it means that we are to take a (relatively) complicated equation that has the "unknown" (often but not always called "x") scattered all over the place and turn it into a (relatively) simple equation with x on the left-hand side by itself and a bunch of other symbols (not including x) on the right-hand side of the "=" sign. Obviously this particular format is "just" a convention. But the idea is independent of the representation: "solve" for the "unknown" quantity, in this case x.

There are a few basic rules we use to "solve" problems in Algebra; these are called "laws" by Mathematicians who want to emphasize that you are not to question their content or representation.

• Definition of Zero:
  

  a - a = 0 (4.2)

  
  

• Definition of Unity:
  

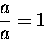  $${a \over a} = 1$$ (4.3)

  
  

• Commutative Laws:^4.5
  

  a + b = b + a (4.4)

  ab = ba (4.5)

  
  

• Distributive Law:
  

  a(b+c) = ab + bc (4.6)

  
  

• Sum or Difference of Two Equations: Adding (or subtracting) the same thing from both sides of an equation gives a new equation that is still OK.
  

  $$\begin{array}[t]{c} ~ \\ + \; ( \\ ~ \end{array} \begin{arr... ...b+a \end{array} \begin{array}[t]{c} ~ \\ ) \\ ~ \end{array}$$ (4.7)

  
  
  
  

  $$% \begin{array}[t]{c} ~ \\ - \; ( \\ ~ \end{array} \begin{a... ...\ d-c \end{array} \begin{array}[t]{c} ~ \\ ) \\ ~ \end{array}$$ (4.8)

  
  

• Product or Ratio of Two Equations: Multiplying (or dividing) both sides of an equation by the same thing also gives a new equation that is still OK.
  

  $$\begin{array}[t]{c} ~ \\ \times \; ( \\ ~ \end{array} \begi... ... ab \end{array} \begin{array}[t]{c} ~ \\ ) \\ ~ \end{array}$$ (4.9)

  
  
  
  

  $$% \begin{array}[t]{c} ~ \\ \div \; ( \\ ~ \end{array} \begi... ...d/c \end{array} \begin{array}[t]{c} ~ \\ ) \\ ~ \end{array}$$ (4.10)

  
  

These "laws" may seem pretty trivial (especially the first two) but they define the rules of Algebra whereby we learn to manipulate the form of equations and "solve" Algebra "problems." We quickly learn equivalent shortcuts like "moving a factor from the bottom of the left-hand-side [often abbreviated LHS] to the top of the right-hand side [RHS]:"

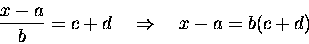$${x - a \over b} = c + d \quad \Rightarrow \quad x - a = b(c+d)$$ (4.11)

and so on; but each of these is just a well-justified concatenation of several of the fundamental steps. (Emergence!)

You may ask, "Why go to so much trouble to express the obvious in such formal terms?" Well, as usual the obvious is not necessarily the truth. While the real, imaginary and complex numbers may all obey these simple rules, there are perfectly legitimate and useful fields of "things" (usually some sort of operators) that do not obey all these rules, as we shall see much later in the course (probably). It is generally a good idea to know your own assumptions; we haven't the time to keep reexamining them constantly, so we try to state them as plainly as we can and keep them around for reference "just in case . . . . "