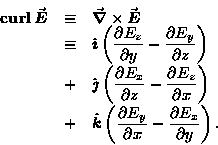

Next: Ampère's Law
Up: Maxwell's Equations
Previous: Gauss' Law
You should now be familiar with
the long integral mathematical form of
FARADAY'S LAW of MAGNETIC INDUCTION:
in SI units,
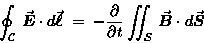 |
(22.5) |
where the line integral of 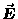 around the closed loop
around the closed loop 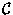 is (by definition) the induced
is (by definition) the induced
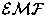 around the loop
and the right hand side refers to the rate of change
of the magnetic flux through the area
around the loop
and the right hand side refers to the rate of change
of the magnetic flux through the area 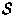 bounded by that closed loop.
bounded by that closed loop.
Figure:
Another infinitesimal volume of space.
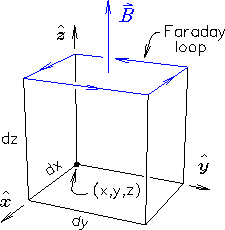 |
To make this easy to visualize, let's again draw an
infinitesimal rectangular box with the z axis along
the direction of the magnetic field, which can be
considered more or less uniform over such a small region.
Then the flux through the "Faraday loop" is just
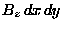 and the line integral of the electric field is
and the line integral of the electric field is
(Yes it is. Study the diagram!)
Here, as before, Ey(x+dx) denotes the magnitude of the y
component of 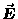 along the front edge of the box, and so on.
As before, we note that
along the front edge of the box, and so on.
As before, we note that
![$[E_y(x+dx) - E_y(x)] = (\dbyd{E_y}{x}) \, dx$](img30.gif) and
and
![$[E_x(y+dy) - E_x(y)] = (\dbyd{E_x}{y}) \, dy$](img31.gif) so that
FARADAY'S LAW reads
so that
FARADAY'S LAW reads
which reduces to the local relationship
between the
"swirlyness" of the spatial dependence
of the electric field and the rate of change of the
magnetic field with time.
If you have studied the definition of the CURL
of a vector field, you may recognize the left-hand side
of the last equation as the z component of
The x and y components of
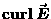 are related to the corresponding components of
are related to the corresponding components of
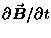 in exactly the same way, allowing us
to write FARADAY'S LAW in a differential form
which describes part of the behaviour of electric and magnetic
fields at every point in space:
in exactly the same way, allowing us
to write FARADAY'S LAW in a differential form
which describes part of the behaviour of electric and magnetic
fields at every point in space:
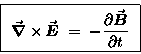 |
(22.6) |
This says, in essence, that any change in the magnetic field
with time induces an electric field perpendicular to the
changing magnetic field. Hold that thought.


Next: Ampère's Law
Up: Maxwell's Equations
Previous: Gauss' Law
Jess H. Brewer -
Last modified: Wed Nov 18 12:31:47 PST 2015
![]() and the line integral of the electric field is
and the line integral of the electric field is