

Up: Maxwell's Equations
Previous: Maxwell's Equations
The two "Laws" of ELECTRODYNAMICS -
FARADAY'S LAW and AMPÈRE'S LAW -
can be combined to produce a very important result.
First let's simplify matters by considering the behaviour
of electromagnetic fields in empty space, where
Our two equations then read
We can simplify further by assuming that the electric field
is in the 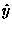 direction and the magnetic field is
in the
direction and the magnetic field is
in the 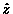 direction. In that case,
direction. In that case,
where the second equation has been multiplied through by 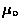 .
.
If we now take the derivative of the first equation with respect to x
and derivative of the second equation with respect to t, we get
the combination of these two equations yields
which the discerning reader will recognize as
the one-dimensional WAVE EQUATION for E,
is the propagation velocity.
You can easily show that there is an identical equation for B.
A more general derivation yields the 3-dimensional version,
In either form, this equation expresses the fact that, since
a changing electric field generates a magnetic field
but that change in the magnetic field generates, in turn,
an electric field, and so on, we can conclude that
electromagnetic fields will propagate spontaneously
through regions of total vacuum in the form of a
wave of 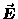 and
and 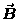 fields working with/against
each other.
fields working with/against
each other.
This startling conclusion (in 1865) led to the revision of
all the "classical" paradigms of Physics,
even such fundamental concepts as space and time.


Up: Maxwell's Equations
Previous: Maxwell's Equations
Jess H. Brewer -
Last modified: Wed Nov 18 12:33:07 PST 2015
