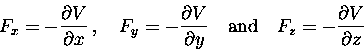

Next: Friction
Up: Potential Energy
Previous: Potential Energy
Physicists so love their ENERGY paradigm that it has been
elevated to a higher status than the original SECOND LAW
from which it was derived! In orer to make this switch, of course,
we had to invent a way of making the reverse derivation
-- i.e. obtaining the vector force
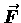 exerted "spontaneously" by the system in question
from the scalar potential energy V of the system.
Here's how: in one dimension we can forget the vector stuff
and just juggle the differentials in
exerted "spontaneously" by the system in question
from the scalar potential energy V of the system.
Here's how: in one dimension we can forget the vector stuff
and just juggle the differentials in
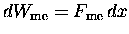 ,
where the
,
where the
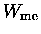 is the work I do in exerting
a force
is the work I do in exerting
a force
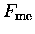 "against the system" through a distance dx.
Assuming that all the work I do against the system
is conserved by the system in the form of its
potential energy V, then
"against the system" through a distance dx.
Assuming that all the work I do against the system
is conserved by the system in the form of its
potential energy V, then
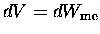 .
On the other hand, the force F exerted by the system
[e.g. the force exerted by the spring] is the equal and opposite
reaction force to the force I exert:
.
On the other hand, the force F exerted by the system
[e.g. the force exerted by the spring] is the equal and opposite
reaction force to the force I exert:
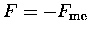 .
The law for conservative forces in one dimension is then
.
The law for conservative forces in one dimension is then
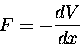 |
(11.15) |
That is, the force of (e.g.) the spring is minus
the rate of change of the potential energy with distance.
In three dimensions this has a little more complicated form,
since
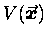 could in principle vary with all three
components of
could in principle vary with all three
components of
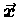 :
x, y and z. We can talk about
the three components independently,
:
x, y and z. We can talk about
the three components independently,
where the notation 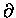 is used to indicate derivatives
with respect to one variable of a function of several
variables [here V(x,y,z)] with the other variables held fixed.
We call
is used to indicate derivatives
with respect to one variable of a function of several
variables [here V(x,y,z)] with the other variables held fixed.
We call
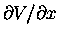 the partial derivative
of V with respect to x.
In the same spirit that moved us to invent vector notation
in the first place [i.e. making the notation more compact],
we use the gradient operator
the partial derivative
of V with respect to x.
In the same spirit that moved us to invent vector notation
in the first place [i.e. making the notation more compact],
we use the gradient operator
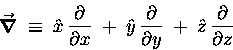 |
(11.16) |
to express the three equations above in one compact form:
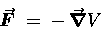 |
(11.17) |
The gradient is easy to visualize in two dimensions:
suppose you are standing on a real hill.
Since your height
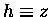 is actually proportional to
your gravitational potential energy Vg,
it is perfectly consistent to view the actual hill as a graph
of the function Vg(x,y) of East-West coordinate x and
North-South coordinate y. In this picture, looking down on the hill
from above, the direction of the gradient
is actually proportional to
your gravitational potential energy Vg,
it is perfectly consistent to view the actual hill as a graph
of the function Vg(x,y) of East-West coordinate x and
North-South coordinate y. In this picture, looking down on the hill
from above, the direction of the gradient
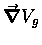 is uphill, and the magnitude of the gradient is the slope
of the hill at the position where the gradient is evaluated.
The nice feature is that
is uphill, and the magnitude of the gradient is the slope
of the hill at the position where the gradient is evaluated.
The nice feature is that
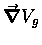 will automatically point "straight up the hill"
-- i.e. in the steepest direction.
Thus
will automatically point "straight up the hill"
-- i.e. in the steepest direction.
Thus
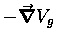 points "straight downhill" - i.e.
in the direction a marble will roll if it is released at that spot!
There are lots of neat tricks we can play with the gradient operator,
but for now I'll leave it to digest.
points "straight downhill" - i.e.
in the direction a marble will roll if it is released at that spot!
There are lots of neat tricks we can play with the gradient operator,
but for now I'll leave it to digest.


Next: Friction
Up: Potential Energy
Previous: Potential Energy
Jess H. Brewer -
Last modified: Sat Nov 14 12:44:29 PST 2015
![]() could in principle vary with all three
components of
could in principle vary with all three
components of
![]() :
x, y and z. We can talk about
the three components independently,
:
x, y and z. We can talk about
the three components independently,