Impulse and Momentum

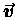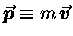Multiplying a scalar times a vector is easy, it just changes its dimensions and length - i.e. it is transformed into a new kind of vector with new units but which is still in the same direction. For instance, when we multiply the vector velocity $\mbox{\boldmath$\vec{v}$\unboldmath }$ by the scalar mass m we get the vector momentum $\mbox{\boldmath$\vec{p}$\unboldmath } \equiv m \, \mbox{\boldmath$\vec{v}$\unboldmath }$ . Let's play a little game with differentials and the SECOND LAW:

$\begin{displaymath}\mbox{\boldmath $\vec{F}$\unboldmath } = {d\mbox{\boldmath $\vec{p}$\unboldmath } \over dt} . \end{displaymath}$

Multiplying both sides by dt and integrating gives

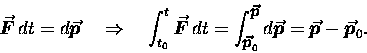$\begin{displaymath}\mbox{\boldmath$\vec{F}$\unboldmath } \, dt = d\mbox{\boldm . . . . . . p}$\unboldmath } - \mbox{\boldmath$\vec{p}$\unboldmath }_0 . \end{displaymath}$

(11.4)

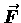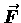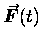The left hand side of the final equation is the time integral of the net externally applied force $\mbox{\boldmath$\vec{F}$\unboldmath }$ . This quantity is encountered so often in Mechanics problems [especially when $\mbox{\boldmath$\vec{F}$\unboldmath }$ is known to be an explicit function of time, $\mbox{\boldmath$\vec{F}$\unboldmath }(t)$ ] that we give it a name:

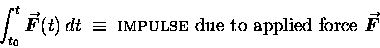$\begin{displaymath}\int_{t_0}^t \mbox{\boldmath$\vec{F}$\unboldmath }(t) \, dt \ . . . . . . due to applied force } \mbox{\boldmath$\vec{F}$\unboldmath } \end{displaymath}$

(11.5)

Our equation can then be read as a sentence:

$$\textstyle \parbox{8cm}{\noindent \lq\lq The {\sl impulse\/} created by the net ext . . . . . . pplied to a system is equal to the {\sl momentum change\/} of the system.$

Next: Conservation of Momentum Up: The Emergence of Mechanics Previous: Antiderivatives

Jess H. Brewer - Last modified: Sat Nov 14 12:39:41 PST 2015