


Next: Hyperfine transitions
Up: Muonic atom collisions
Previous: Elastic scattering
Due to the differences in the binding
energies, the muon can be transferred to the heavier isotopes:
 |
(2) |
where
 is the isotope splitting
(Table 1.1) due to the reduced mass difference.
The subscript n denotes the possibility of transfer from excited
states (Section 1.2.4).
In the D/T mixture target, the rate of muon transfer from the ground state of
the deuterium atom to the triton
is the isotope splitting
(Table 1.1) due to the reduced mass difference.
The subscript n denotes the possibility of transfer from excited
states (Section 1.2.4).
In the D/T mixture target, the rate of muon transfer from the ground state of
the deuterium atom to the triton
 is relatively slow (
is relatively slow (
 s-1) and becomes one of the bottle-necks at low tritium
concentrations. It should be noted that the released energy, divided
between two projectiles, gives an acceleration to the muonic atom in the lab
frame corresponding to the energy
s-1) and becomes one of the bottle-necks at low tritium
concentrations. It should be noted that the released energy, divided
between two projectiles, gives an acceleration to the muonic atom in the lab
frame corresponding to the energy
 |
(3) |
The energy dependent calculations predict that
 is
significantly larger at higher energies (more than about 10 eV). This may be
exploited, for example, by triple isotope mixture targets
(H/D/T) [27], in which a faster reaction, muon transfer from
a proton to a deuteron, creates an energetic
is
significantly larger at higher energies (more than about 10 eV). This may be
exploited, for example, by triple isotope mixture targets
(H/D/T) [27], in which a faster reaction, muon transfer from
a proton to a deuteron, creates an energetic 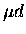 ,
thus effectively
speeding up the transfer to tritium.
,
thus effectively
speeding up the transfer to tritium.
Figure 1.2:
Scattering cross sections for 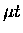 with a hydrogen
isotope nuclei from the Nuclear Atlas [16,17], showing
the Ramsauer-Townsend minimum at around 10 eV for
with a hydrogen
isotope nuclei from the Nuclear Atlas [16,17], showing
the Ramsauer-Townsend minimum at around 10 eV for  .
.
 cross sections plotted include both elastic and spin exchange
reactions, where
cross sections plotted include both elastic and spin exchange
reactions, where 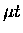 (0) is the singlet state and
(0) is the singlet state and 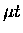 (1) is
the triplet state.
(1) is
the triplet state.
 |



Next: Hyperfine transitions
Up: Muonic atom collisions
Previous: Elastic scattering

![]() is
significantly larger at higher energies (more than about 10 eV). This may be
exploited, for example, by triple isotope mixture targets
(H/D/T) [27], in which a faster reaction, muon transfer from
a proton to a deuteron, creates an energetic
is
significantly larger at higher energies (more than about 10 eV). This may be
exploited, for example, by triple isotope mixture targets
(H/D/T) [27], in which a faster reaction, muon transfer from
a proton to a deuteron, creates an energetic ![]() ,
thus effectively
speeding up the transfer to tritium.
,
thus effectively
speeding up the transfer to tritium.
