BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Gauss' Law

If you go on in Physics you will learn all about GAUSS' LAW along with vector calculus in your advanced course on ELECTRICITY AND MAGNETISM, where it is used to calculate the electric field strength at various distances from highly symmetric distributions of electric charge. However, GAUSS' LAW can be applied to a huge variety of interesting situations having nothing to do with electricity except by analogy. Moreover, the rigourous statement of GAUSS' LAW in the mathematical language of vector calculus is not the only way to express this handy concept, which is one of the few powerful modern mathematical tools which can be accurately deduced from "common sense" and which really follows from a statement so simple and obvious as to seem trivial and uninteresting, to wit:

(Colloquial form of GAUSS' LAW)
 
"When something passes out of a region,
it is no longer inside that region."

How, you may ask, can such a dumb tautology teach us anything we don't already know? The power of GAUSS' LAW rests in its combination with our knowledge of geometry (e.g. the surface area  A  of a sphere of radius  r  is 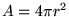  $A = 4\pi r^2$) and our instinctive understanding of symmetry (e.g. there is no way for a point of zero size to define a favoured direction ). When we put these two skills together with GAUSS' LAW we are able to easily derive some not-so-obvious quantitative properties of many commonly-occurring natural phenomena.