 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE
Trigonometry is a specialized branch of Geometry in which we pay
excruciatingly close attention to the properties of triangles,
in particular right triangles.
Referring to Fig. 4.2 again, we define the sine
of the angle ![]() (abbreviated
(abbreviated
![]() )
to be the
ratio of the "far side" a to the hypotenuse c
and the cosine of
)
to be the
ratio of the "far side" a to the hypotenuse c
and the cosine of ![]() (abbreviated
(abbreviated
![]() )
to be the ratio of the "near side" b to the hypoteneuse c:
)
to be the ratio of the "near side" b to the hypoteneuse c:
| (4.12) |
tangent:For the life of me, I can't imagine why anyone invented the cotangent, the secant and the cosecant -- as far as I can tell, they are totally superfluous baggage that just slows you down in any actual calculations. Forget them. [Ahhhh. I have always wanted to say that! Of course you are wise enough to take my advice with a grain of salt, especially is you want to appear clever to Mathematicians....]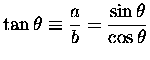
cotangent: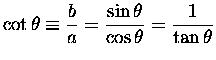
secant: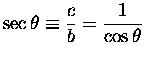
cosecant: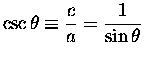
The sine and cosine of ![]() are our
trigonometric workhorses. In no time at all, I will be
wanting to think of them as functions - i.e.
when you see "
are our
trigonometric workhorses. In no time at all, I will be
wanting to think of them as functions - i.e.
when you see "
![]() " I will want you to say,
"cosine of theta" and think of it as
" I will want you to say,
"cosine of theta" and think of it as
![]() the same way you think of y(x). Whether as simple ratios
or as functions, they have several delightful properties,
the most important of which is obvious from the
Pythagorean Theorem:4.6
the same way you think of y(x). Whether as simple ratios
or as functions, they have several delightful properties,
the most important of which is obvious from the
Pythagorean Theorem:4.6
| (4.13) |
I will need other trigonometric identities later on, but they can wait - why introduce math until we need it? [I have made an obvious exception in this Chapter as a whole only to "jump start" your Mathematical language (re)training.]