BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Maxwell's Equations

In 1865, James Clerk Maxwell assembled all the known "Laws" of in their most compact, elegant (differential) form, shown here in SI units:

GAUSS' LAW FOR ELECTROSTATICS:

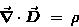$$\Div{D} \; = \; \rho$$ (22.9)

GAUSS' LAW FOR MAGNETOSTATICS:

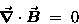$$\Div{B} \; = \; 0$$ (22.10)

FARADAY'S LAW:

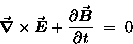$$\Curl{E} + {\partial \Vec{B} \over \partial t} \; = \; 0$$ (22.11)

AMPÈRE'S LAW:

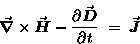$$\Curl{H} - {\partial \Vec{D} \over \partial t} \; = \; \Vec{J}$$ (22.12)

These four basic equations are known collectively as MAXWELL'S EQUATIONS; they are considered by most Physicists to be a beautifully concise summary of phenomenology.

Well, actually, a complete description of also requires two additional laws:

EQUATION OF CONTINUITY:

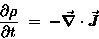$${\partial \rho \over \partial t} \; = \; - \Div{J}$$ (22.13)

LORENTZ FORCE:

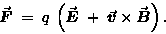$$\Vec{F} \; = \; q \, \left( \Vec{E} \; + \; \Vec{v} \times \Vec{B} \right) .$$ (22.14)