BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: The Spring Pendulum
Up: Simple Harmonic Motion
Previous: Projecting the Wheel
The above mechanical example serves to introduce the idea of
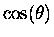 and
and
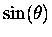 as functions
in the sense to which we have (I hope) now become accustomed.
In particular, if we realize that (by definition)
as functions
in the sense to which we have (I hope) now become accustomed.
In particular, if we realize that (by definition)
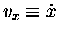 and
and
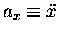 ,
the formulae for vx(t) and ax(t)
represent the derivatives of x(t):
,
the formulae for vx(t) and ax(t)
represent the derivatives of x(t):
| x |
= |
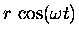 |
(13.4) |
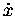 |
= |
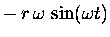 |
(13.5) |
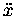 |
= |
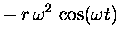 |
(13.6) |
-- which in turn tell us the derivatives of the sine and cosine functions:
So if we want we can calculate the
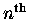 derivative
of a sine or cosine function almost as easily as we did for
our "old" friend the exponential function.
I will not go through the details this time, but this feature
again allows us to express these functions as
series expansions:
derivative
of a sine or cosine function almost as easily as we did for
our "old" friend the exponential function.
I will not go through the details this time, but this feature
again allows us to express these functions as
series expansions:
![\begin{displaymath}\begin{array}[c]{rcccccc}
\exp(z) =& 1 &+ z &+ \onehalf z^2 . . .
. . . \sin(z) =& & z & &- {1 \over 3!} z^3
& &+ \cdots
\end{array}\end{displaymath}](img33.gif) |
(13.9) |
where I have shown the exponential function along with the
sine and cosine for reasons that will soon be apparent.


Next: The Spring Pendulum
Up: Simple Harmonic Motion
Previous: Projecting the Wheel
Jess H. Brewer -
Last modified: Sun Nov 15 13:35:44 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE 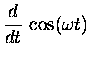
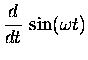
![\begin{displaymath}\begin{array}[c]{rcccccc}
\exp(z) =& 1 &+ z &+ \onehalf z^2 . . .
. . . \sin(z) =& & z & &- {1 \over 3!} z^3
& &+ \cdots
\end{array}\end{displaymath}](img33.gif)