Next: Magnetic Interactions
Up: Orbital Angular Momentum
Previous: Orbital Angular Momentum
One of Niels Bohr's main contributions to Physics
was his assertion (backed up by experiment) that
angular momentum is quantized -
it can only occur in integer multiples of 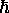 .
Erwin Schr´'odinger showed why this was true for
the wave functions of the hydrogen atom, but by that
time Bohr's principle had been elevated to an empirical
"law" of Physics that went well beyond the realm of atoms.
Schr´'odinger also showed the peculiar nature of the
quantization of
.
Erwin Schr´'odinger showed why this was true for
the wave functions of the hydrogen atom, but by that
time Bohr's principle had been elevated to an empirical
"law" of Physics that went well beyond the realm of atoms.
Schr´'odinger also showed the peculiar nature of the
quantization of  : first, its magnitude obeys
: first, its magnitude obeys
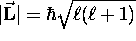 where
where
 can only have integer values from zero to
can only have integer values from zero to
 , n being the principle quantum number
for which
, n being the principle quantum number
for which 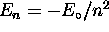 in the case of hydrogen;
second, its projection onto the z axis obeys
in the case of hydrogen;
second, its projection onto the z axis obeys
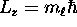 where
where 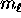 can take on
only integer values from
can take on
only integer values from 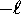 to
to 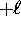 .
Note that Bohr's original prescription for angular
momentum quantization (integer multiples of
.
Note that Bohr's original prescription for angular
momentum quantization (integer multiples of 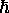 )
is actually applicable to the z component
of
)
is actually applicable to the z component
of  - its projection
onto the z
quantization axis, which is chosen arbitrarily
unless there is a magnetic field applied, in which case
- its projection
onto the z
quantization axis, which is chosen arbitrarily
unless there is a magnetic field applied, in which case
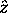 is always chosen along the field,
is always chosen along the field,
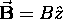 .
.
Jess H. Brewer -
Last modified: Mon Nov 23 13:55:25 PST 2015
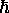 .
Erwin Schr´'odinger showed why this was true for
the wave functions of the hydrogen atom, but by that
time Bohr's principle had been elevated to an empirical
"law" of Physics that went well beyond the realm of atoms.
Schr´'odinger also showed the peculiar nature of the
quantization of
.
Erwin Schr´'odinger showed why this was true for
the wave functions of the hydrogen atom, but by that
time Bohr's principle had been elevated to an empirical
"law" of Physics that went well beyond the realm of atoms.
Schr´'odinger also showed the peculiar nature of the
quantization of  : first, its magnitude obeys
: first, its magnitude obeys
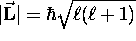 where
where
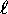 can only have integer values from zero to
can only have integer values from zero to
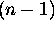 , n being the principle quantum number
for which
, n being the principle quantum number
for which 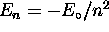 in the case of hydrogen;
second, its projection onto the z axis obeys
in the case of hydrogen;
second, its projection onto the z axis obeys
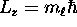 where
where 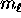 can take on
only integer values from
can take on
only integer values from 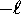 to
to 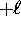 .
Note that Bohr's original prescription for angular
momentum quantization (integer multiples of
.
Note that Bohr's original prescription for angular
momentum quantization (integer multiples of 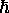 )
is actually applicable to the z component
of
)
is actually applicable to the z component
of  - its projection
onto the z
quantization axis, which is chosen arbitrarily
unless there is a magnetic field applied, in which case
- its projection
onto the z
quantization axis, which is chosen arbitrarily
unless there is a magnetic field applied, in which case
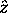 is always chosen along the field,
is always chosen along the field,
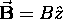 .
.