- Definition:
The rate of change [slope] of a function at a point
is the limiting value of its average slope
over an interval including that point,
as the width of the interval shrinks to zero:
All the remaining Laws and Rules can be proven by
algebraic manipulation of this definition.
- Operator Notation:
The symbol
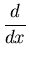 (read "derivative with respect to x")
can be thought of as a mathematical "verb"
(called an operator)
which "operates on" whatever we place to its right.
Thus
(read "derivative with respect to x")
can be thought of as a mathematical "verb"
(called an operator)
which "operates on" whatever we place to its right.
Thus
- Power Law:
The simplest class of derivatives are those of power-law functions:
valid for all powers p, whether positive, negative,
integer, rational, irrational, real, imaginary or complex.
- Product Law:
The derivative of the product of two functions is not
the product of their derivatives! Instead,
- Constant times a Function:
The Product Law gives
where a is a constant (i.e., not a function of x).
This is often referred to as
"pulling the constant factor outside the derivative."
- Function of a Function:
Suppose y is a function of x and x is in turn a function of t.
- Exponentials:
where k is any constant.
- Natural Logarithms:
- Antiderivatives:
We can "solve" integrals or "antiderivatives"
the same way we "solve" long division problems:
by trial and error guessing!
Suppose we are given an explicit function f(x)
[for example,
f(x) = x2] and told that
f(x) is the derivative of a function y(x)
which we would like to know - that is,
Well, we know that
so we must divide by 3 to get
where the constant term y0 (the value of y when x=0)
cannot be determined from the information given -
the derivative of any constant is zero, so such an integral
is always undetermined to within such a constant of integration.
Jess H. Brewer
2004-02-13