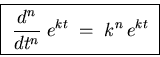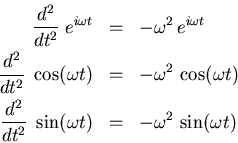It is helpful to remember the definition of the exponential function
in terms of a power series:
If we let x be imaginary,
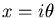 (where
(where 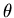 is real),
then this can be written
is real),
then this can be written
which ought to remind you (doesn't it?) of the series expansions for
the sinusoidal functions:
Note that these expansions perform a sort of "leapfrog" between
even and odd terms. Putting them all together we can easily see that
and, since
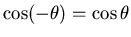 while
while
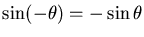 ,
,
These simple equivalences are, to my mind, among the most
astonishing relationships in all of mathematics.
Why? Because they show an intimate relationship
between two functions which would seem at first glance
to have absolutely nothing in common: the monotonically
increasing or decreasing exponential function 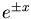 and the sinusoidally oscillating
and the sinusoidally oscillating 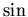 and
and 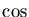 functions!
functions!
We can also invert the relationship and obtain a definition
for the 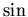 and
and 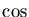 functions in terms of exponentials:
functions in terms of exponentials:
Let's review the most important (for Physics, anyway)
property of the exponential function: it is its own derivative!
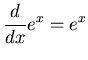 .
If x = kt then we "pull out an extra factor of k"
with each derivative with respect to t:
.
If x = kt then we "pull out an extra factor of k"
with each derivative with respect to t:
This latter property (which, by the way, works just as well
for complex k as for real k) establishes the connection between
the derivatives of
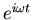 (for instance) and those of
(for instance) and those of
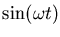 and
and
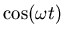 :
:
You will recall how useful these second-derivative properties were
in SIMPLE HARMONIC MOTION and WAVES.
Well, you ain't seen nothing yet!
Jess H. Brewer -
Last modified: Sun Nov 15 13:59:42 PST 2015
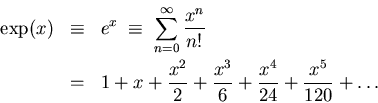
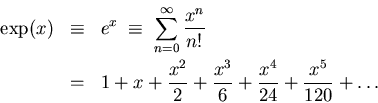
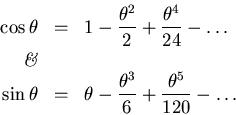
![]() and
and ![]() functions in terms of exponentials:
functions in terms of exponentials:
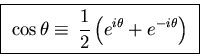
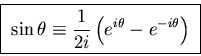
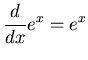 .
If x = kt then we "pull out an extra factor of k"
with each derivative with respect to t:
.
If x = kt then we "pull out an extra factor of k"
with each derivative with respect to t: