Next:
Counting Modes in 1D
The wavenumber 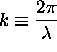 of a wave has a special significance in both classical and quantum physics.
Because waves are quantized (they can only occur in "packets" of
energy
of a wave has a special significance in both classical and quantum physics.
Because waves are quantized (they can only occur in "packets" of
energy 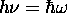 and momentum
and momentum
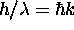 )
we are often in the position of asking what possible values
k can have, and counting the number of allowed
k values.
From this procedure arises the notion of " k-space" and the
density of states in k-space, which may seem rather exotic
on the first encounter but with which every physicist ultimately
becomes intimately familiar.
)
we are often in the position of asking what possible values
k can have, and counting the number of allowed
k values.
From this procedure arises the notion of " k-space" and the
density of states in k-space, which may seem rather exotic
on the first encounter but with which every physicist ultimately
becomes intimately familiar.
The following arguments apply to any sort of wave
(or wavefunction) that is confined to a finite region
and constrained to have nodes at the boundaries.
Jess H. Brewer -
Last modified: Mon Nov 23 17:24:53 PST 2015
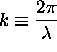 of a wave has a special significance in both classical and quantum physics.
Because waves are quantized (they can only occur in "packets" of
energy
of a wave has a special significance in both classical and quantum physics.
Because waves are quantized (they can only occur in "packets" of
energy 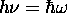 and momentum
and momentum
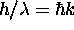 )
we are often in the position of asking what possible values
k can have, and counting the number of allowed
k values.
From this procedure arises the notion of " k-space" and the
density of states in k-space, which may seem rather exotic
on the first encounter but with which every physicist ultimately
becomes intimately familiar.
)
we are often in the position of asking what possible values
k can have, and counting the number of allowed
k values.
From this procedure arises the notion of " k-space" and the
density of states in k-space, which may seem rather exotic
on the first encounter but with which every physicist ultimately
becomes intimately familiar.