- . . . temperature?1
-
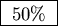 .
This is where
.
This is where 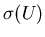 has a maximum, and therefore zero slope. The inverse of zero
is
has a maximum, and therefore zero slope. The inverse of zero
is
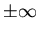 .
There is no difference between
.
There is no difference between
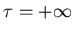 and
and
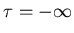 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ``hottest''?2
-
At
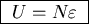 (n=N).
The slope of
(n=N).
The slope of 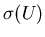 has its steepest negative value there,
meaning that entropy is gained by losing U.
has its steepest negative value there,
meaning that entropy is gained by losing U.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . . 3
-
At that U the temperature
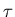 has its
smallest negative value.
has its
smallest negative value.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . answers]4
-
(i)
 (
(
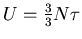 )
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . molecules?5
-
The average velocity is proportional to the square root of temperature
and to the inverse square root of the mass of the particle,
so the ratio of average velocities of He and O2 is the
square root of the ratio of the mass of an oxygen molecule to
that of a helium atom:
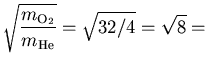
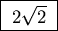 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Explain. 6
-
The gravitational and electrostatic forces have the same
dependence on the distance between the electron and proton, so
they will never be equal. Their ratio will
always be
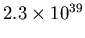 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Explain. 7
-
 .
There is no net charge inside the sphere,
so by Gauss' Law there is no net flux of
.
There is no net charge inside the sphere,
so by Gauss' Law there is no net flux of
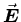 out through
the closed surface. If the net flux is zero, its average
over the surface is too.
out through
the closed surface. If the net flux is zero, its average
over the surface is too.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . sentences:8
-
The electric field inside the slab is zero.
The electric field outside but very close to the surface of the slab
is normal (perpendicular) to the surface of the slab.
The electric field outside but very close to the surface of the slab
has a magnitude
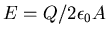 .
.
The electric field at a distance 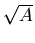 from the surface of the slab
cannot be determined from the information given.
from the surface of the slab
cannot be determined from the information given.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . inert.9
-
The gravitational potential energy of a buckyball is
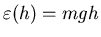 where h is the altitude above sea level.
If our ``system'' is just the altitude of the buckyball,
then in thermal equilibrium the BOLTZMANN DISTRIBUTION
implies that the probability of finding one buckyball at height h
is proportional to
where h is the altitude above sea level.
If our ``system'' is just the altitude of the buckyball,
then in thermal equilibrium the BOLTZMANN DISTRIBUTION
implies that the probability of finding one buckyball at height h
is proportional to
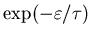 where
where
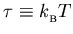 .
Since all buckyballs share the same probability distribution,
the density D(h) of buckyballs has this same distribution.
We don't need to know the normalization to find the ratio
.
Since all buckyballs share the same probability distribution,
the density D(h) of buckyballs has this same distribution.
We don't need to know the normalization to find the ratio
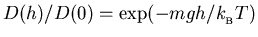 .
This ratio will be
e-1 when
.
This ratio will be
e-1 when
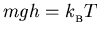 or when
or when
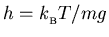 .
Plugging in the numbers gives
.
Plugging in the numbers gives
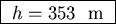 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . )?10
-
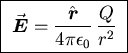 as for any isotropic charge distribution viewed from outside.
as for any isotropic charge distribution viewed from outside.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
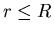 )?11
)?11
-
Here it is a little more complicated. First we need to know
the constant of proportionality a in
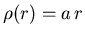 :
since
:
since
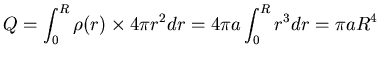 ,
we have
,
we have
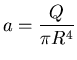 .
Now imagine a spherical Gaussian surface at r<R.
The total charge within that closed surface
is
.
Now imagine a spherical Gaussian surface at r<R.
The total charge within that closed surface
is
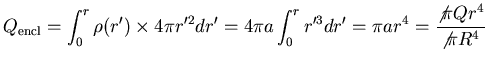 and the integral of
and the integral of
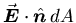 over that surface is
over that surface is
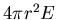 ,
so Gauss' Law gives
,
so Gauss' Law gives
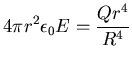 or
or
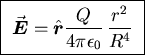 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
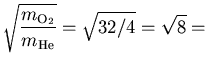
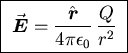 as for any isotropic charge distribution viewed from outside.
as for any isotropic charge distribution viewed from outside.
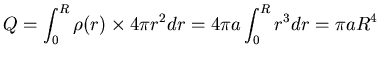 ,
we have
,
we have
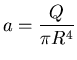 .
Now imagine a spherical Gaussian surface at r<R.
The total charge within that closed surface
is
.
Now imagine a spherical Gaussian surface at r<R.
The total charge within that closed surface
is
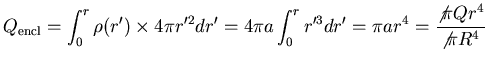 and the integral of
and the integral of
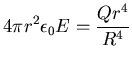 or
or
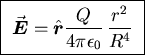 .
.