- . . . plates?1
- ANSWER: The electric field is reduced
by a factor of
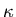 , giving
E = 100/310 or
, giving
E = 100/310 or
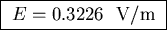 .
For simple effects like this, a long explanation is unnecessary.
Derivations need not be reproduced if you understand their results.
.
For simple effects like this, a long explanation is unnecessary.
Derivations need not be reproduced if you understand their results.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . resistances?2
- ANSWER:
R1 + R2 = 16 [1] or
R2 = 16 - R1 [1a].
R1-1 + R2-1 = 1/3 [2] or
 [2a] or,
substituting [1],
[2a] or,
substituting [1],
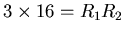 [2b] or,
substituting [1a],
48 = R1 (16 - R1) [2c] or,
collecting terms by powers of R1,
R12 - 16 R1 + 48 = 0 [2d], from which the Quadratic Theorem
gives
[2b] or,
substituting [1a],
48 = R1 (16 - R1) [2c] or,
collecting terms by powers of R1,
R12 - 16 R1 + 48 = 0 [2d], from which the Quadratic Theorem
gives
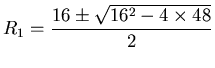 so that
so that
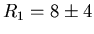 . Pick one sign for R1 and the other for R2:
. Pick one sign for R1 and the other for R2:
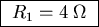 and
and
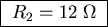 .
Quite a few people jumped over all the algebra to the correct answers.
I would be grateful if someone could explain to me how this is possible.
.
Quite a few people jumped over all the algebra to the correct answers.
I would be grateful if someone could explain to me how this is possible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . closed?3
- ANSWER: All six capacitors see the same voltage (1 V)
and have the same capacitance (1 F) so each has the same charge (1 C)
and the total charge is
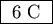 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
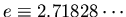 ]4
]4
- ANSWER:
By symmetry, no capacitor can ``get ahead'' of any of the others,
so we have basically one big 6 F capacitor being drained through
3 resistors in parallel on each side. Each set of 3 resistors has
an effective resistance of R/3 and they are in series, so the
overall effective resistance is 2R/3. The time constant is thus
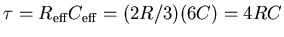 or
or
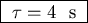 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
Explain.5
- ANSWER:
 . That capacitor would have a different
time constant from the others, and the others would be affected as well.
This was intended as a hint for the preceding
question, where symmetry is essential to the argument.
Surprisingly, many people gave self-contradictory answers;
it seems the phrase, ``Would there be an unique answer . . . ''
was frequently misunderstood. Again, I would be grateful
if someone could explain this confusion to me.
. That capacitor would have a different
time constant from the others, and the others would be affected as well.
This was intended as a hint for the preceding
question, where symmetry is essential to the argument.
Surprisingly, many people gave self-contradictory answers;
it seems the phrase, ``Would there be an unique answer . . . ''
was frequently misunderstood. Again, I would be grateful
if someone could explain this confusion to me.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . 1 C.6
- ANSWER:
 .
The capacitor is already fully charged to
.
The capacitor is already fully charged to
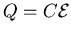 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . uncharged.7
- ANSWER: An uncharged capacitor is ``like a short''
so the current initially flows as if it weren't there:
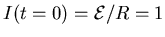 A. Then as the
capacitor charges up, its charge asymptotically
approaches Qf = 1 C as
A. Then as the
capacitor charges up, its charge asymptotically
approaches Qf = 1 C as
 .
The time constant is
.
The time constant is
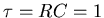 s. Algebraically,
s. Algebraically,
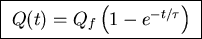 .
Many people omitted all quantitative information,
despite the provision of numerical values for all
relevant quantities and the emphasis on ``in detail''.
I have emphasized the importance of doing one's
calculations in terms of algebraic symbols until the
very end, but then you should recognize whether
a quantitative answer is called for.
.
Many people omitted all quantitative information,
despite the provision of numerical values for all
relevant quantities and the emphasis on ``in detail''.
I have emphasized the importance of doing one's
calculations in terms of algebraic symbols until the
very end, but then you should recognize whether
a quantitative answer is called for.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Tesla]?8
- ANSWER:
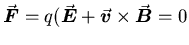 (no deflection) if
(no deflection) if
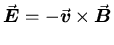 .
Since all three vectors are mutually perpendicular, this means
the magnitudes must obey E = v B or
.
Since all three vectors are mutually perpendicular, this means
the magnitudes must obey E = v B or
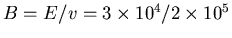 or
or
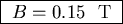 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . constant.9
- ANSWER: This is actually a trivial question, embedded in a
complicated context to see if you can remember the simple ideas
under pressure. Since the Lorentz force is proportional to
the cross product of the velocity with the magnetic field, it is
perpendicular to both; thus a magnetic field can change the
direction of the velocity, but never its
magnitude. Without a change in speed,
the kinetic energy cannot change either.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . words.)10
- ANSWER:
By Ampère's Law, the field outside the whole cable (r>R) is zero,
because the same current links any Ampèrian loop in both
directions, canceling out. Inside the outer shell (r<R) only the
central conductor's current links the loop, so the magnetic field goes
around the wire in circles in a direction given by the Right Hand Rule
(RHR): if the thumb of your right hand points along the current in
the inner wire, its fingers curl around the wire in the direction of
the magnetic field - i.e. down in front and up on the back side.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . . 11
- ANSWER: Since the outer conductor plays no role for an
Ampèrian loop with r<R, in this region the field is given by
the familiar result for a simple wire:
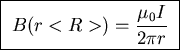 .
Outside, as stated earlier, the field is zero:
.
Outside, as stated earlier, the field is zero:
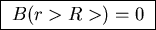 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . meters).12
- ANSWER:
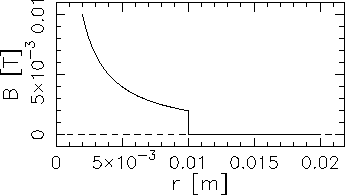
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . motion.13
- This
is not the usual orientation in which a pole vaulter would hold
the pole during a ``run up,'' but this sprinter is performing
a Physics experiment, so unconventional behaviour is expected!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . other?14
- ANSWER: This can be solved several ways.
You can imagine the pole to be part of a rectangular Faraday loop
where the opposite side is stationary; so the area of the loop
is increasing at a rate
dA/dt = Lv where L=6 m and v=7 m/s
and the magnetic flux through the loop is therefore increasing
at a rate
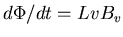 where
where
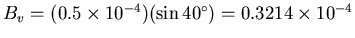 T. Thus the potential
developed around the loop (i.e. across the pole) is
T. Thus the potential
developed around the loop (i.e. across the pole) is
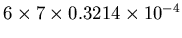 =
=
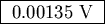 .
.
Or you can imagine a charge q in the wire in the pole,
moving along at horizontal speed v through a vertical magnetic field
component
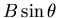 , and thus experiencing a Lorentz force
, and thus experiencing a Lorentz force
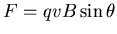 along the pole. If this force were to
move the charge from one end of the pole to the other, it would
do work
along the pole. If this force were to
move the charge from one end of the pole to the other, it would
do work
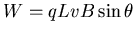 ; thus the potential created by
the Lorentz force is
; thus the potential created by
the Lorentz force is
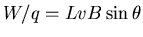 , giving the same
answer as before.
, giving the same
answer as before.
Quite a few people got their trigonometry mixed up (or failed to
read the question carefully); I gave more marks for understanding
the basic principles than for flawless algebra or arithmetic.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 [2a] or,
substituting [1],
[2a] or,
substituting [1],
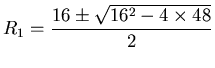 so that
so that
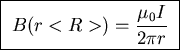 .
Outside, as stated earlier, the field is zero:
.
Outside, as stated earlier, the field is zero:
