Next:
Sines, Cosines and Exponentials
COMPLEX EXPONENTIALS
In your first exposure to simple harmonic motion
and waves you probably saw only the real
sinusoidal functions 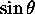 and
and 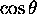 (where
(where 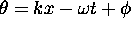 ,
the phase of an oscillation).
This was reasonable enough, since all the phenomena of
classical mechanics are in fact real,
at least in the mathematical sense.
Whether they are real in the colloquial sense
is subject to discussion....
,
the phase of an oscillation).
This was reasonable enough, since all the phenomena of
classical mechanics are in fact real,
at least in the mathematical sense.
Whether they are real in the colloquial sense
is subject to discussion....
In quantum mechanics, which we claim describes the
way the real world really works,
things are not always real in the mathematical sense.
Well, ``things'' are always real, if by ``things'' you mean
physical observables, but the things you have to talk about
to make predictions about the real ``things''
- or at least about what you are likely to measure if
you observe one - those things are not real;
they are almost always complex. Sort of like
that sentence, eh? No, mathematically complex.
That is, complex in the mathematical sense, i.e.
having a real part and an imaginary part.
With that introduction to quantum mechanics
I should have produced the proper state of confusion
one needs to approach the subject. But for now
I would like to demonstrate a few simple properties
of the most remarkable function ever invented:
the exponential function, 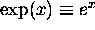 .
.
Jess Brewer
Sat Sep 14 17:53:55 PDT 1996
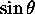 and
and 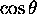 (where
(where 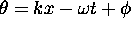 ,
the phase of an oscillation).
This was reasonable enough, since all the phenomena of
classical mechanics are in fact real,
at least in the mathematical sense.
Whether they are real in the colloquial sense
is subject to discussion....
,
the phase of an oscillation).
This was reasonable enough, since all the phenomena of
classical mechanics are in fact real,
at least in the mathematical sense.
Whether they are real in the colloquial sense
is subject to discussion....
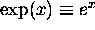 .
.