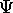 ?
It is the function which gives all the information
that there is about a quantum system.
A quantum system can be one or many particles.
?
It is the function which gives all the information
that there is about a quantum system.
A quantum system can be one or many particles.
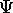 .
It is called the probability amplitude because
the square of its absolute value is the
probability density
.
It is called the probability amplitude because
the square of its absolute value is the
probability density 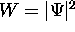 .
This probability W tells us whether the quantum particle
is likely to be in a certain state or location.
If W is large then the probability is high.
If W approaches zero then the probability approaches zero.
If we integrate the probability density over all space,
the total probability must be 1.
A good reference discussing the wave function and wave packets
etc. is Ch. 6 in ``The Emperor's New Mind''
by Roger Penrose.
.
This probability W tells us whether the quantum particle
is likely to be in a certain state or location.
If W is large then the probability is high.
If W approaches zero then the probability approaches zero.
If we integrate the probability density over all space,
the total probability must be 1.
A good reference discussing the wave function and wave packets
etc. is Ch. 6 in ``The Emperor's New Mind''
by Roger Penrose.
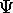 ?
In principle we can use
?
In principle we can use 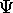 to calculate all the properties
of any physical system. We can use it to calculate particle position,
momentum, energy .... We can use it to calculate atomic structure,
the behaviour of solids, liquids, gases and plasmas.
We can describe elementary particles, lasers, superconductivity
etc.
to calculate all the properties
of any physical system. We can use it to calculate particle position,
momentum, energy .... We can use it to calculate atomic structure,
the behaviour of solids, liquids, gases and plasmas.
We can describe elementary particles, lasers, superconductivity
etc.
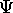 particular to different types of particles?
There are basically two types of particles:
bosons and fermions.
We will talk about that in a bit.
We don't have to worry about it yet.
The spatial part of the wave functions that we are talking about now
will be the same for both types of particles.
What is different for different particles
(that we are talking about now) is their mass
and their electric charge.
If they have no mass ( e.g. photons),
then they have no dispersion which means
the phase velocity is the same as the group velocity.
If they do have mass then they will have some dispersion
(see discussion of wave packets and dispersion further on).
particular to different types of particles?
There are basically two types of particles:
bosons and fermions.
We will talk about that in a bit.
We don't have to worry about it yet.
The spatial part of the wave functions that we are talking about now
will be the same for both types of particles.
What is different for different particles
(that we are talking about now) is their mass
and their electric charge.
If they have no mass ( e.g. photons),
then they have no dispersion which means
the phase velocity is the same as the group velocity.
If they do have mass then they will have some dispersion
(see discussion of wave packets and dispersion further on).
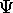 just a neat trick?
No, it's not. It or something like it is necessary.
As we said, to represent a free particle of fixed energy
(or k ), you need a
just a neat trick?
No, it's not. It or something like it is necessary.
As we said, to represent a free particle of fixed energy
(or k ), you need a 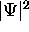 that is uniform, that is
the probability of finding the particle is
the same everywhere. But at the same time that
function
that is uniform, that is
the probability of finding the particle is
the same everywhere. But at the same time that
function 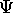 must be able to produce wave-like
interference effects. The only way anyone knows how to do this
is to use the complex probability amplitude function.
must be able to produce wave-like
interference effects. The only way anyone knows how to do this
is to use the complex probability amplitude function.
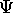 for this wave packet function,
it will be zero everywhere expect one small region
of space and time.
for this wave packet function,
it will be zero everywhere expect one small region
of space and time.
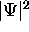 .
And of course since it is a probability,
sometimes you have to measure it lots of times.
We will see, though, that the situation is not always
as vague as it appears in the two-slit experiment.
.
And of course since it is a probability,
sometimes you have to measure it lots of times.
We will see, though, that the situation is not always
as vague as it appears in the two-slit experiment.
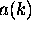 ?
When you are adding up waves of different wavelength
to make a localized wave packet,
?
When you are adding up waves of different wavelength
to make a localized wave packet,
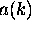 tells you
how much of each wavelength (
tells you
how much of each wavelength (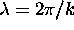 )
to use.
)
to use.
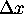 and
and
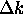 .
For the Gaussian, the contribution of
a given value of k to the wave packet is proportional to
.
For the Gaussian, the contribution of
a given value of k to the wave packet is proportional to
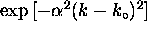 where
where 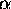 and
and
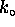 are constants.
This factor times some constant is the function
are constants.
This factor times some constant is the function
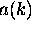 .
Then the wave packet function is just the integral
.
Then the wave packet function is just the integral
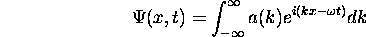
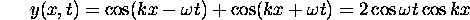
For all times the function 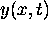 has nodes at kx = odd multiples of
has nodes at kx = odd multiples of
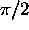 .
.
Expectation Values
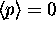 , but
, but
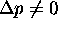 .
This is discussed below.
.
This is discussed below.
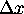 and
and
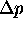 differ?
The method isn't really different, it only looks that way.
This is because we have chosen the Schrödinger representation
and in that picture the wave function is defined as
a function of space and time ( i.e. x and t ).
So then it is easy to find
differ?
The method isn't really different, it only looks that way.
This is because we have chosen the Schrödinger representation
and in that picture the wave function is defined as
a function of space and time ( i.e. x and t ).
So then it is easy to find 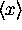 and
and 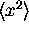 .
Finding
.
Finding 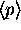 and
and
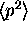 is a little harder (see next question), but the method for
finding the expectation value is the same.
Note that if we chose a momentum - frequency representation
instead of a space - time representation
then the momentum expectation value would look simple and the
position one would look more complicated.
is a little harder (see next question), but the method for
finding the expectation value is the same.
Note that if we chose a momentum - frequency representation
instead of a space - time representation
then the momentum expectation value would look simple and the
position one would look more complicated.
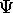 in the probability integral, produces an expectation value for
that quantity In the Schrödinger representation.
The operator for x is just x , for
in the probability integral, produces an expectation value for
that quantity In the Schrödinger representation.
The operator for x is just x , for
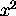 it is just
it is just
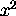 .
But for momentum we have to find a way to write p
in terms of x or t , so that we can do the integral
.
But for momentum we have to find a way to write p
in terms of x or t , so that we can do the integral

The trick we found was to note that

This then says that we can do the integral by equating
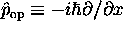 ,
the momentum operator in the Schrödinger representation.
,
the momentum operator in the Schrödinger representation.
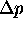 must be zero.
Then shouldn't
must be zero.
Then shouldn't 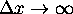 ?
No. Just because
?
No. Just because 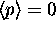 doesn't necessarily
mean that
doesn't necessarily
mean that 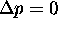 .
For the ``stationary'' states in the well
the magnitude of the momentum is not on average zero.
We know this because we calculated
.
For the ``stationary'' states in the well
the magnitude of the momentum is not on average zero.
We know this because we calculated
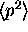 and found that was not zero. Also remember this is the same as
saying the particle has kinetic energy, which it does.
The reason
and found that was not zero. Also remember this is the same as
saying the particle has kinetic energy, which it does.
The reason 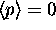 is because on average
the particle is moving to the right the same amount of time
it is moving to the left.
is because on average
the particle is moving to the right the same amount of time
it is moving to the left.
Square Potential Wells
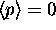 then why is the probability exponential?
See comments about
then why is the probability exponential?
See comments about 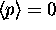 above.
The fact that the average of the momentum is zero
doesn't mean the magnitude of the momentum is zero.
above.
The fact that the average of the momentum is zero
doesn't mean the magnitude of the momentum is zero.
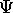 and its first spatial derivative
must be continuous smooth functions.
and its first spatial derivative
must be continuous smooth functions.