The Finite Square Well



reveal many of the qualitative characteristics of quantum mechanical (QM) systems.
THINK FIRST!
The first step in any problem is to gather together all your qualitative knowledge about the situation before you start working out any quantitative details. This is especially true in QM, where the ``blind calculation'' approach is often not only a waste of effort but actually intractable!
SYMMETRY:
In this case we save ourselves a mind-bogglingly difficult
mathematical nightmare by making a few simple observations
about symmetry: the potential
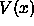 is symmetric
about x = 0; this implies that the probability of finding
the particle on one side of the well must be equal to
the probability of finding it on the other side.
Since the wavefunction
is symmetric
about x = 0; this implies that the probability of finding
the particle on one side of the well must be equal to
the probability of finding it on the other side.
Since the wavefunction 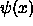 is squared
to get this probability, it follows that
is squared
to get this probability, it follows that
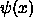 can be either an even function of x
can be either an even function of x
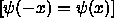 or an odd
function of x
or an odd
function of x 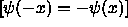 .
This places lots of constraints on
.
This places lots of constraints on
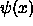 for which we will soon be grateful.
for which we will soon be grateful.
BOUND or UNBOUND?
A potential well generally has bound states
of well-defined energy E < 0 unless the mass is too small
(see below).
There is also a continuum of unbound states with E > 0,
whose behaviour we may also want to examine.
[For instance, the classical particle will ``pass over''
the well and continue on the other side every time;
this will not be the case for the QM result!]
We will start with the bound state
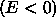 .
If
.
If 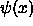 is localized around the potential well,
then to be normalizable it must obey
is localized around the potential well,
then to be normalizable it must obey
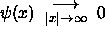 .
[Moreover, we certainly expect
.
[Moreover, we certainly expect 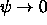 as we get further into regions where the
classical particle cannot penetrate at all
due to its inadequate energy!]
Our first guess for such functions
is always the decaying exponential function, here
as we get further into regions where the
classical particle cannot penetrate at all
due to its inadequate energy!]
Our first guess for such functions
is always the decaying exponential function, here
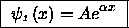 (2)
for region 1
(2)
for region 1 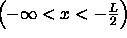 .
[Remember, x = -|x| in this region.]
Since we are always free to choose the overall phase
of
.
[Remember, x = -|x| in this region.]
Since we are always free to choose the overall phase
of 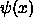 arbitrarily [multiplying by a constant factor
of
arbitrarily [multiplying by a constant factor
of 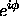 has no effect on the physics],
we may do so immediately by choosing that
has no effect on the physics],
we may do so immediately by choosing that
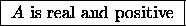 .
In this case the
.
In this case the 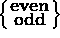 symmetry requirement
gives two possible solutions for region 3
symmetry requirement
gives two possible solutions for region 3
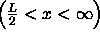 :
:
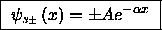 where the + sign is for the symmetric ( even) solution
and the - sign is for the antisymmetric ( odd) solution.
where the + sign is for the symmetric ( even) solution
and the - sign is for the antisymmetric ( odd) solution.
On region 2 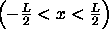 we expect some sort of oscillatory function,
for which the obvious
we expect some sort of oscillatory function,
for which the obvious 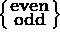 choices are
choices are
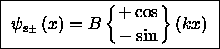 (3)
where the - sign is chosen for the ( odd)
(3)
where the - sign is chosen for the ( odd)
 function
for the following reason:
function
for the following reason:
BOUNDARY CONDITIONS:
We must always satisfy the matching condition
for the wavefunction [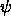 must be continuous]
and the matching condition for its spatial derivative
[
must be continuous]
and the matching condition for its spatial derivative
[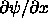 must also be continuous (except where
the potential is infinite)]
at the boundaries
must also be continuous (except where
the potential is infinite)]
at the boundaries 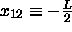 and
and 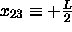 .
The first matching condition immediately implies that
.
The first matching condition immediately implies that
 must be positive at
must be positive at 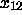 ,
since we chose
,
since we chose 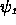 positive.
For the odd function this mandates the negative sign
in Eq. (3) above.
If we now explicitly apply the matching condition
for
positive.
For the odd function this mandates the negative sign
in Eq. (3) above.
If we now explicitly apply the matching condition
for 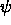 at the boundaries, we get
at the boundaries, we get
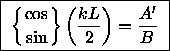 (4)
where
(4)
where 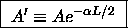 is the magnitude of
is the magnitude of 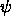 at the boundary.
The matching condition for the derivative gives
at the boundary.
The matching condition for the derivative gives
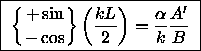 (5).
Dividing Eq. (5) by Eq. (4) gives
(5).
Dividing Eq. (5) by Eq. (4) gives
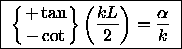 (6).
Adding the squares of Eqs. (4) and (5) gives
(6).
Adding the squares of Eqs. (4) and (5) gives
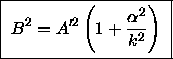 (7).
(7).
APPLYING the SCHRÖDINGER EQUATION:
How do these guesses fare with our original equation?
On regions 1 and 3 we get
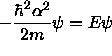 ,
which ensures
,
which ensures
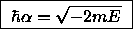 (8)
since E < 0 is the same throughout.
On region 2 we have
(8)
since E < 0 is the same throughout.
On region 2 we have
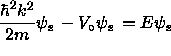 or
or
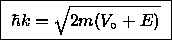 (9).
Substituting these values for
(9).
Substituting these values for 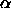 and k
back into Eqs. (7) and (6) gives
and k
back into Eqs. (7) and (6) gives
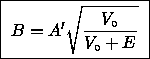 (10)
and
(10)
and 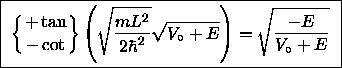 (11),
respectively.
(11),
respectively.
Equation (11) implies restrictions on the allowed values of E.
This is anticipated [remember, E is quantized]
but you may be surprised to find a transcendental
equation governing E. There is no algebraic solution
to Eq. (11)! [Actually, Eq. (11) is two transcendental
equations for 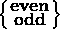
 .
As n and
.
As n and  increase,
we alternate between even and odd solutions.]
If we define
increase,
we alternate between even and odd solutions.]
If we define 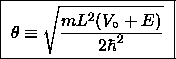 and
and
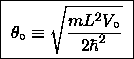 then Eq. (11) reads
then Eq. (11) reads 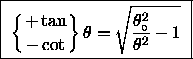 ,
which one can plot up and solve graphically for the
allowed values of
,
which one can plot up and solve graphically for the
allowed values of 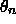 (and therefore
(and therefore 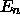 ).
For a detailed description of how to do this,
see pp. 156-162 of French & Taylor,
An Introduction to Quantum Physics.
).
For a detailed description of how to do this,
see pp. 156-162 of French & Taylor,
An Introduction to Quantum Physics.
ARE THERE ANY BOUND STATES?
Under what circumstances does Eq. (11) have a solution?
On the one hand, the general rule that confinement costs
energy would seem to dictate that a narrower well must be
deeper in order to ``hang on to'' a particle:
smaller L (or m)
should require larger 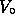 .
The definition of
.
The definition of 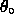 reflects this aspect of the problem:
reflects this aspect of the problem:
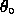 is smaller
for smaller
is smaller
for smaller 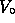 and/or smaller
and/or smaller 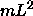 .
However,
.
However, 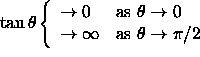 while
while
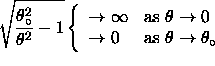 , so that
the two must intersect somewhere, no matter how small
, so that
the two must intersect somewhere, no matter how small
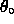 is.
Thus there is always at least one
(even) bound state for this potential!
The apparent paradox is resolved when we realize that
the exponentially decaying ``tails'' of
is.
Thus there is always at least one
(even) bound state for this potential!
The apparent paradox is resolved when we realize that
the exponentially decaying ``tails'' of
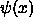 penetrate deeper and deeper into the classically forbidden region
as
penetrate deeper and deeper into the classically forbidden region
as 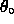 gets smaller and smaller, until the region
where
gets smaller and smaller, until the region
where 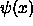 is sinusoidal (inside the well) becomes a
negligible point at the centre of a wavefunction
that decays away exponentially from a centre cusp!
The stability of this solution
is extremely sensitive to the ``flatness'' of V = 0 in regions
far from the well, for obvious reasons.
is sinusoidal (inside the well) becomes a
negligible point at the centre of a wavefunction
that decays away exponentially from a centre cusp!
The stability of this solution
is extremely sensitive to the ``flatness'' of V = 0 in regions
far from the well, for obvious reasons.
An interesting limit is obtained by allowing the well
to shrink 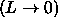 while holding constant the ratio
while holding constant the ratio
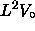 (so that
(so that 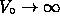 in compensation).
This is called the delta function potential.
in compensation).
This is called the delta function potential.
IS THAT THE WHOLE STORY??
After all this work, what have we learned?
We know 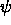 everywhere to within a normalization constant A
which can be found by applying
everywhere to within a normalization constant A
which can be found by applying
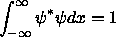 if we need it
( if we want to calculate expectation values)
and we have what we need to find
if we need it
( if we want to calculate expectation values)
and we have what we need to find
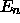 (and therefore
(and therefore 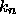 and
and 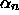 ) for the
stationary states allowed in this potential well.
It would be nice to have a tidy algebraic solution,
but even simple problems are not necessarily nice!
If you want exact solutions, you will have to solve the
transcendental equations each time you specify the
parameters
) for the
stationary states allowed in this potential well.
It would be nice to have a tidy algebraic solution,
but even simple problems are not necessarily nice!
If you want exact solutions, you will have to solve the
transcendental equations each time you specify the
parameters 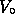 ,
L and m which govern the
physics of this problem. However, it is possible to
make many qualitative obervations (see class notes)
based on simple right-hemisphere graphical arguments.
We may also examine some limiting cases:
,
L and m which govern the
physics of this problem. However, it is possible to
make many qualitative obervations (see class notes)
based on simple right-hemisphere graphical arguments.
We may also examine some limiting cases:
DEEPLY BOUND STATES:
If 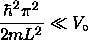 ,
the lowest few eigenstates will have energies
,
the lowest few eigenstates will have energies
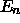 that are only a little above the bottom of the well
[
that are only a little above the bottom of the well
[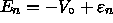 ,
where
,
where  ].
Then Eq. (11) reads approximately
].
Then Eq. (11) reads approximately
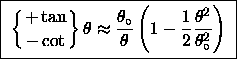 or, even more approximately,
or, even more approximately,
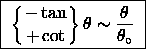 .
You may want to play with this approximation to see
the spectrum of deeply-bound states.
Note that
.
You may want to play with this approximation to see
the spectrum of deeply-bound states.
Note that 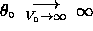 ,
so in the limit of the infinite square well
the solutions are simply
,
so in the limit of the infinite square well
the solutions are simply
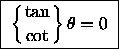 ,
which is satisfied for
,
which is satisfied for 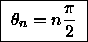 .
Check that this agrees with the formula you know already,
bearing in mind that here we have defined the top
of the well to have V = 0....
.
Check that this agrees with the formula you know already,
bearing in mind that here we have defined the top
of the well to have V = 0....
UNBOUND STATES:
In all the equations above we have assumed E < 0 (bound states).
What happens when E > 0?
Taking the equations at face value,
we would conclude that 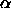 is imaginary,
meaning that our initial assumption of exponentially decaying
solutions outside the well was incorrect and that
is imaginary,
meaning that our initial assumption of exponentially decaying
solutions outside the well was incorrect and that
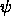 must be sinusoidal (oscillatory) everywhere.
This is precisely the case. See how far you can get
assuming that what we have written so far still applies....
must be sinusoidal (oscillatory) everywhere.
This is precisely the case. See how far you can get
assuming that what we have written so far still applies....