- Starting with Maxwell's equations in differential form, derive Maxwell's equations in integral form.
- Starting with Maxwell's generalization of Ampère's Law,
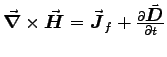 , derive the continuity equation,
, derive the continuity equation, 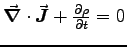 ,
which is the mathematical expression of charge conservation.
,
which is the mathematical expression of charge conservation.
- Starting with Maxwell's equations in free space
(
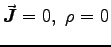 ), show that
), show that 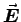 and
and 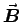 each satisfy a wave equation. What is the speed of propagation
of the resulting wave in each case?
each satisfy a wave equation. What is the speed of propagation
of the resulting wave in each case?

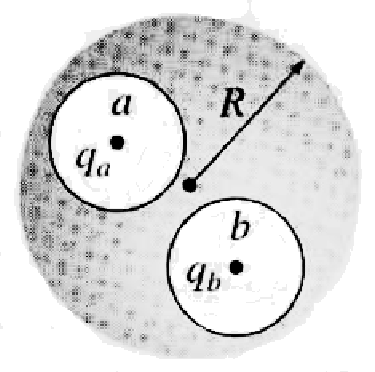
6. If a third charge qc were brought near the conductor, which (if any) would change:
(i) ![]() ?
?
(ii) ![]() ?
?
(ii) ![]() ?
?
(iv) The electric fields inside cavities a and b?
(v) The electric field outside the conductor?
- Show that the electric field is radial and is the same in the dielectric half as in the vacuum half of the capacitor.
- Deduce the capacitance per unit length of this coaxial capacitor.
- If the conductors carry free charges per unit length
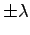 ,
find the polarization
,
find the polarization 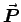 in the dielectric
at any point a distance r from the central axis, in terms of
in the dielectric
at any point a distance r from the central axis, in terms of
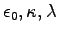 and r.
and r.


Hint: Note that this situation has cylindrical symmetry (not spherical!), with no z dependence, and hence simplifies to a 2-D plane polar problem.