Please review Section 10.1 and Ch. 12.
- (p. 420, Problem 10.3) - GIVEN V &
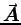 . . .
Find the
. . .
Find the 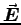 ,
, 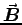 ,
, 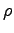 &
& 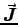 corresponding to
corresponding to
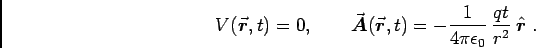
- POINT CHARGE:
- Find the
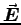 and
and 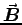 fields corresponding to
a stationary point charge q situated at the origin.
fields corresponding to
a stationary point charge q situated at the origin.
- State the charge and current distributions of this situation.
- What are the electric and magnetic potentials?
- Is there any relation between this situation
and that described in Problem 10.3?
- (p. 420, Problem 10.5) - GAUGE TRANSFORMATION:
Use the gauge function
to transform the potentials in Problem 10.3, and
comment on the result.
- WHICH GAUGE?
- In Problem 10.3 above,
are the potentials in the Coulomb gauge, the Lorentz gauge,
both, or neither?
- In Problem 2 above, are the potentials in the Coulomb gauge,
the Lorentz gauge, both, or neither?
- NATURAL UNITS:
Since c is now a defined quantity that keeps
appearing in confusing places in our notation for 4-vectors etc.,
and since nanoseconds (ns) are perfectly handy units
for distance, it seems silly to not just measure time and
distance in the same units (seconds) and set c=1.
While we're at it, why not set the ubiquitous constant in
quantum mechanics to unity as well (
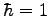 ) so that all
angular momenta are unitless and (because
) so that all
angular momenta are unitless and (because
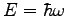 )
energies are measured in s-1?
)
energies are measured in s-1?
- In what units would we then measure velocities, momenta,
masses, forces and accelerations?
- Suppose we set the Coulomb force constant
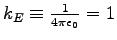 as well. In what units would we then measure charge, electric field,
magnetic field, and potentials V and
as well. In what units would we then measure charge, electric field,
magnetic field, and potentials V and 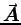 ?
?
- Write out Maxwell's equations in this system of units.
(Hint: We must have
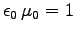 .)1
.)1
- 4-POTENTIAL:
In Eq. (12.131) on p. 541, Griffiths states that,
"As you might guess, V and
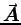 together
constitute a 4-vector:
together
constitute a 4-vector:
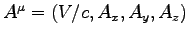 ."
This is a very strong statement with profound consequences.
You can't just take any 3-vector and combine it with a
convenient scalar in the same units to make a true 4-vector!
Explain why we should believe this about
."
This is a very strong statement with profound consequences.
You can't just take any 3-vector and combine it with a
convenient scalar in the same units to make a true 4-vector!
Explain why we should believe this about 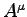 ,
and list any essential conditions that must be met
for it to be true.
,
and list any essential conditions that must be met
for it to be true.
Jess H. Brewer
2006-01-24
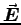 and
and 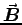 fields corresponding to
a stationary point charge q situated at the origin.
fields corresponding to
a stationary point charge q situated at the origin.
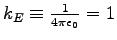 as well. In what units would we then measure charge, electric field,
magnetic field, and potentials V and
as well. In what units would we then measure charge, electric field,
magnetic field, and potentials V and 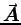 ?
?
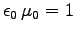 .)1
.)1