- Suppose you embedded some free charge in a piece of glass. About how long would it take for the charge to flow to the surface?
- Silver is an excellent conductor, but it's expensive. Suppose you were designing a microwave experiment to operate at a frequency of 1010 Hz. How thick would you make the silver coatings?
- Find the wavelength and propagation speed in copper for radio waves at 1 MHz. Compare the corresponding values in air (or vacuum).
- Show that the skin depth in a poor conductor
(
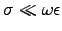 ) is
) is
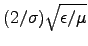 (independent of frequency).
Find the skin depth (in meters) for (pure) water.2
(independent of frequency).
Find the skin depth (in meters) for (pure) water.2
- Show that the skin depth in a good conductor
(
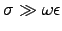 ) is
) is 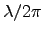 (where
(where 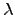 is the wavelength in the conductor.
Find the skin depth (in nanometers) for a typical metal
[
is the wavelength in the conductor.
Find the skin depth (in nanometers) for a typical metal
[
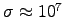 (
(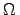 m)-1]
in the visible range (
m)-1]
in the visible range (
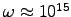 s-1),
assuming
s-1),
assuming
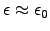 and
and
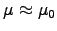 .
Why are metals opaque?
.
Why are metals opaque?
- Show that in a good conductor the magnetic field
lags the electric field by 45
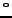 ,
and find the ratio of their amplitudes.
For a numerical example, use the "typical metal"
in the previous question.
,
and find the ratio of their amplitudes.
For a numerical example, use the "typical metal"
in the previous question.
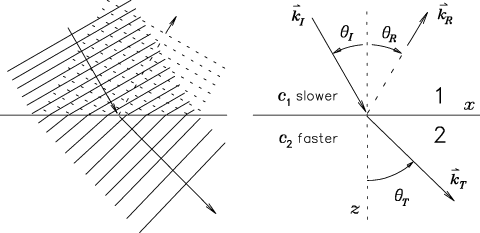
A quick way to construct the evanescent wave is simply to quote the results of Sect. 9.3.3, with
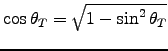 is imaginary. (Obviously,
is imaginary. (Obviously, - Show that
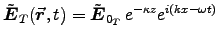 ,
where
,
where
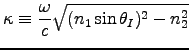 and
and
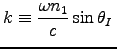 .
This describes a wave propagating in the x direction
(parallel to the interface!)
and attenuated in the z direction.
.
This describes a wave propagating in the x direction
(parallel to the interface!)
and attenuated in the z direction.
- Noting that
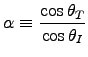 is now imaginary,
use Eqs. (9.109),
is now imaginary,
use Eqs. (9.109),
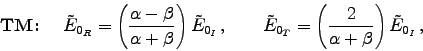
to calculate the reflection coefficient for polarization parallel to the plane of incidence. [Notice that you get 100% reflection, which is better than at a conducting surface (see for example Problem 9.21).] - Do the same for polarization perpendicular to the plane of incidence
(use the results of Problem 9.16):
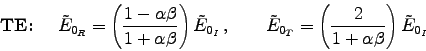
- In the case of polarization perpendicular to the plane of incidence,
show that the (real) evanescent fields are
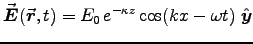 ,
,
![${\displaystyle \Vec{B}(\Vec{r},t) = (E_0/\omega) \,
e^{-\kappa z} [ \kappa \sin (kx - \omega t) \; \Hat{x} \; + \;
k \cos (kx - \omega t) \; \Hat{z} ] }$](img32.gif) .
.
- Check that the fields in the last part satisfy all of MAXWELL'S EQUATIONS (9.67).
- For those same fields, construct the Poynting vector and show that, on average, no energy is transmitted in the z direction.