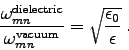
Thus, for a given operating frequency, a dielectric filled waveguide can be smaller than an empty one.
- Show directly that Eqs. (9.197) satisfy MAXWELL'S EQUATIONS (9.177) and the boundary conditions (9.175).
- Find the net charge per unit length,
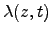 ,
and the net current, I(z,t), on the inner conductor.
,
and the net current, I(z,t), on the inner conductor.
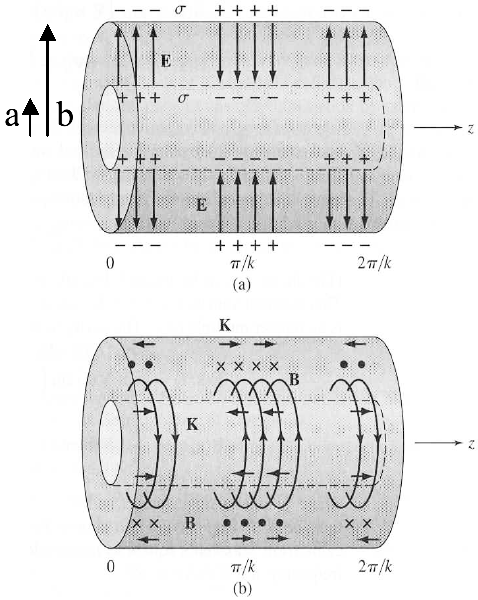
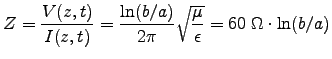
In general, the characteristic impedance of a transmission line is given by
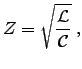
Show that the characteristic impedance of this
coax line satisfies this definition by calculating
![]() and
and ![]() explicitly, and then Z.
explicitly, and then Z.