![\begin{displaymath}
\hbox{\rm Equation (11.14), } \qquad
V(r,\theta,t) = - {p_0 . . .
. . . ght)
\sin\left[\omega\left(t - {r \over c}\right)\right] \, ,
\end{displaymath}](img1.gif)
can be expressed in "coordinate-free" form by writing
![\begin{displaymath}
\hbox{\rm (11.18), } \qquad
\Vec{E}(r,\theta,t) = - {\muz p . . .
. . . ft[\omega\left(t - {r \over c}\right)\right] \Hat{\theta} \, ,
\end{displaymath}](img4.gif)
![\begin{displaymath}
\hbox{\rm (11.19), } \qquad
\Vec{B}(r,\theta,t) = - {\muz p . . .
. . . left[\omega\left(t - {r \over c}\right)\right] \Hat{\phi} \, ,
\end{displaymath}](img5.gif)
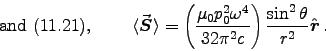
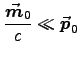 for an atom with magnetic dipole moment
for an atom with magnetic dipole moment
- In terms of the variables given
(not all of which may be relevant, of course)
find the formula for the intensity of the radiation at ground level,
a distance R away from the base of the tower.
You may assume that
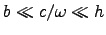 .
[Note: we are interested only in the magnitude
of the radiation, not in its direction -
when measurements are taken, the detector will be aimed
directly at the antenna.]
.
[Note: we are interested only in the magnitude
of the radiation, not in its direction -
when measurements are taken, the detector will be aimed
directly at the antenna.]
- How far from the base of the tower should the engineer have made the measurement? What is the formula for the intensity at this location?
- KRUD's actual power output is 35 kilowatts, its frequency is 90 MHz, the antenna's radius is 6 cm, and the height of the tower is 200 m. The city's radio-emission limit is 200 microwatts/cm2. Is KRUD in compliance?
- Find the formula for the total power radiated,
in terms of the following parameters:
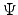 (the angle between the geographic and magnetic north poles),
M (the magnitude of the Earth's magnetic dipole moment),
and
(the angle between the geographic and magnetic north poles),
M (the magnitude of the Earth's magnetic dipole moment),
and 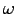 (the angular velocity of rotation of the Earth).
[Hint: refer to Prob. 11.4 or Prob. 11.12.]
(the angular velocity of rotation of the Earth).
[Hint: refer to Prob. 11.4 or Prob. 11.12.]
- Using the fact that the Earth's magnetic field is about half a gauss at the Equator, estimate the magnetic dipole moment M of the Earth.
- Find the power radiated. [Your answer should be several times 10-5 W.]
- Pulsars are thought to be rotating neutron stars,
with a typical radius of about
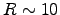 km,
a typical surface magnetic field of
km,
a typical surface magnetic field of 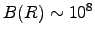 T
and a variety of rotational periods T; let's use
T
and a variety of rotational periods T; let's use 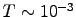 s.
What sort of radiated power would you expect from such a star?
[See J.P. Ostriker and J.E. Gunn, Astrophys. J. 157,
1395 (1969). Answer:
2 x 1036 W.]
s.
What sort of radiated power would you expect from such a star?
[See J.P. Ostriker and J.E. Gunn, Astrophys. J. 157,
1395 (1969). Answer:
2 x 1036 W.]