Find the radiation resistance of the wire joining the two ends of the oscillating electric dipole described in Section 11.1.2. (This is the resistance that would give the same average power loss - to heat - as the oscillating dipole in fact puts out in the form of radiation.) Show that
Find the radiation resistance for the oscillating magnetic dipole shown in Fig. 11.8. Express your answer in terms of
- Suppose an electron decelerates at a constant rate a
from some initial velocity v0 down to zero.
What fraction of its initial kinetic energy is lost to EM radiation?
(The rest is absorbed by whatever mechanism
keeps the acceleration constant.) Assume
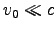 (nonrelativistic case) so that the Larmor formula can be used.3
(nonrelativistic case) so that the Larmor formula can be used.3
- To get a sense of the numbers involved, suppose the initial velocity is thermal4 (around 105 m/s) and the distance over which the electron decelerates to rest is 30 Å. What can you conclude about radiation losses for electrons in an ordinary conductor?
Consider a half-wave linear antenna of length
- Show that the linear charge density is
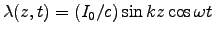 ,
(i.e. the charge density is maximum at the times when
the current is zero.)
,
(i.e. the charge density is maximum at the times when
the current is zero.)
- If an FM radio station broadcasts at a frequency of 10 MHz with a power of 10 kW from a half-wave antenna, how long must the antenna be? What is the current?