THE UNIVERSITY OF BRITISH COLUMBIA
Physics 401
Assignment #
1:
REVIEW
SOLUTIONS:
Wed. 04 Jan. 2006 - finish by Wed. 11 Jan.
This first assignment was just for review, to make sure you hadn't
forgotten (or could quickly recall) what you learned in PHYS 301/354
(or earlier) about the E&M covered in the first 7 chapters
of our textbook: David Griffiths, "Introduction to Electrodynamics".
Almost all you need is on the inside front and back covers
of the textbook:
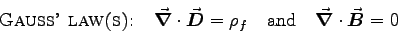 |
(1) |
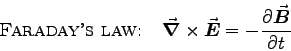 |
(2) |
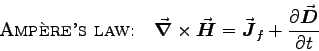 |
(3) |
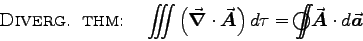 |
(4) |
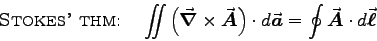 |
(5) |
- MAXWELL'S EQUATIONS:
- Starting with Maxwell's equations in differential form,
derive Maxwell's equations in integral form.
ANSWER: Applying (4) to
 yields
yields 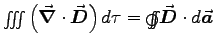 .
Plug in (1) to give
.
Plug in (1) to give
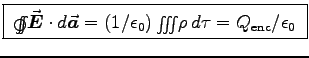 .
Similarly for
.
Similarly for 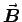 with
with 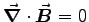 to give
to give
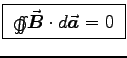 .
We use (5) [also known as the CURL THEOREM]
on
.
We use (5) [also known as the CURL THEOREM]
on 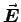 to give
to give
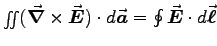 and plug in (2) to get
and plug in (2) to get
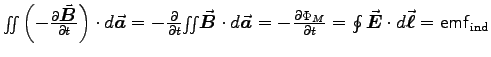 or
or
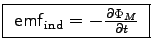 .
Finally we apply (5) to
.
Finally we apply (5) to  to get
to get
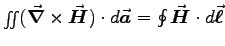 and plug in (3) to get
and plug in (3) to get
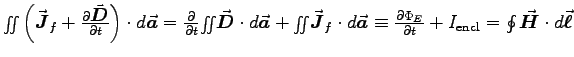 or
or
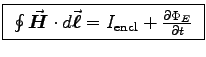 .
.
- Starting with Maxwell's generalization of Ampère's Law,
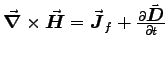 , derive the continuity equation,
, derive the continuity equation, 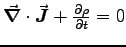 ,
which is the mathematical expression of charge conservation.
ANSWER: Just take the divergence of both sides of Eq. (3),
remembering that the divergence of a curl is always zero, and plug in
GAUSS' LAW for
,
which is the mathematical expression of charge conservation.
ANSWER: Just take the divergence of both sides of Eq. (3),
remembering that the divergence of a curl is always zero, and plug in
GAUSS' LAW for 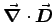 (see above). Immediately we have
(see above). Immediately we have
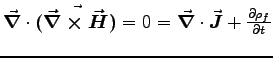 which is the same
as the CONTINUITY EQUATION if we note that
which is the same
as the CONTINUITY EQUATION if we note that
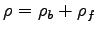 where
where 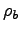 is the (unchanging) bound charge density.
is the (unchanging) bound charge density.
- Starting with Maxwell's equations in free space
(
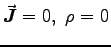 ), show that
), show that 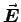 and
and 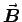 each satisfy a wave equation. What is the speed of propagation
of the resulting wave in each case?
ANSWER:
First take the time derivative of Eq. (2) to get
each satisfy a wave equation. What is the speed of propagation
of the resulting wave in each case?
ANSWER:
First take the time derivative of Eq. (2) to get
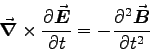 |
(6) |
(where the order of differentiation
wrt time and space have been reversed). Then substitute
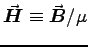 and
and
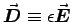 into Eq. (3) and take its curl to get
into Eq. (3) and take its curl to get
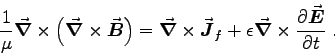 |
(7) |
Expanding the double curl gives 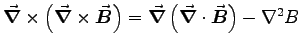 and GAUSS' LAW
says
and GAUSS' LAW
says 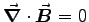 , so Eq. (7) becomes
, so Eq. (7) becomes
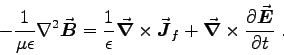 |
(8) |
At this point you were expected to impose the usual conditions
for propagating EM waves, namely no free charges or currents
(
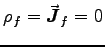 ). In a conductor, things get
a bit more complicated (see Section 9.4 of the textbook).
With
). In a conductor, things get
a bit more complicated (see Section 9.4 of the textbook).
With 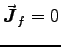 , Eq. (8) has the same RHS
(right hand side) as the LHS of Eq. (6), yielding
, Eq. (8) has the same RHS
(right hand side) as the LHS of Eq. (6), yielding
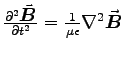 or
or
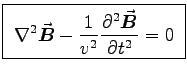
- i.e. the WAVE EQUATION for 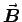 ,
where the speed of propagation is
,
where the speed of propagation is
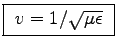 .
In free space, of course,
.
In free space, of course,
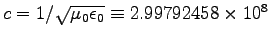 m/s [exactly, by definition].
Since
m/s [exactly, by definition].
Since 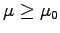 and
and
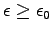 ,
, 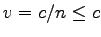 ,
where
,
where
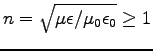 is the index of refraction.
is the index of refraction.
For 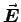 we take the time derivative of Eq. (3),
with
we take the time derivative of Eq. (3),
with
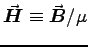 and
and
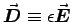 ,
this time setting
,
this time setting 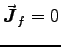 at the outset. The result is
at the outset. The result is
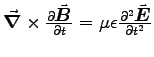 .
Then we take the curl of Eq. (2) to get
.
Then we take the curl of Eq. (2) to get
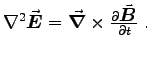 Again matching up RHS with LHS gives
Again matching up RHS with LHS gives
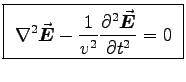
- i.e. the same WAVE EQUATION for 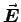 .
.
- CHARGED CONDUCTORS:
Two spherical cavities, of radii a and b, are hollowed out
from the interior of a solid neutral conducting sphere of radius R,
as shown in the figure. There are charges qa and qb
at the centres of the respective cavities.

- What is the electric field in the solid (shaded) conducting material?
ANSWER:
 .
.
- Find the surface charges
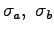 and
and 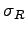 at the respective surfaces. ANSWER: Since the point charges are
centered on the spherical cavities, by GAUSS' LAW it takes
an equal and opposite uniform surface charge to cancel
at the respective surfaces. ANSWER: Since the point charges are
centered on the spherical cavities, by GAUSS' LAW it takes
an equal and opposite uniform surface charge to cancel 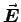 inside the conductor. Thus
inside the conductor. Thus
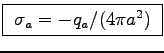 and
and
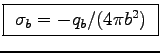 .
The net interior surface charge, -(qa+qb), leaves behind a
charge +(qa+qb) which will distribute itself uniformly over
the outer surface (to achieve maximum separation), giving an
exterior surface charge of
.
The net interior surface charge, -(qa+qb), leaves behind a
charge +(qa+qb) which will distribute itself uniformly over
the outer surface (to achieve maximum separation), giving an
exterior surface charge of
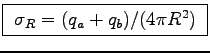 .
.
- What is the electric field outside the conductor
at a distance r>R from the centre of the large sphere?
ANSWER:
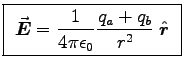 .
.
- What are the electric fields inside cavities a and b?
ANSWER:
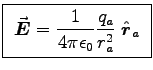 and
and
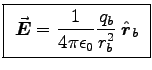 ,
where ra and rb are the distances from the centre of each cavity,
respectively.
,
where ra and rb are the distances from the centre of each cavity,
respectively.
- What are the forces on qa and qb?
ANSWER:
 . They are centred in their cavities.
. They are centred in their cavities.
- If a third charge qc were brought near the conductor,
which (if any) would change:
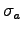 ?
?  .
.
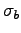 ?
?  .
.
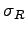 ?
?  . An additional (nonuniform)
surface charge would be required to terminate electric field lines
coming from the third charge.
. An additional (nonuniform)
surface charge would be required to terminate electric field lines
coming from the third charge.
- The electric fields inside cavities a and b?
 .
.
- The electric field outside the conductor?
 . Doh!
. Doh!
- COAXIAL CAPACITOR:
A capacitor is constructed of two very long concentric cylindrical
conductors with their common axis horizontal, as shown in the diagram.
The space between them is exactly half filled with
a linear dielectric liquid with dielectric constant
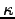 .
.
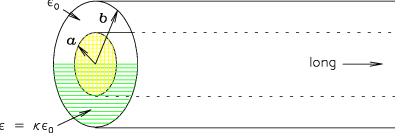
- Show that the electric field is radial
and is the same in the dielectric half
as in the vacuum half of the capacitor.
ANSWER: Symmetry with respect to z ensures that
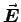 can have only radial and aximuthal components Er and
can have only radial and aximuthal components Er and 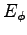 and that neither one changes with z.
[I am using r rather than the textbook's s for the radial direction.]
Meanwhile each of the conductors is at constant potential,
forcing cylindrical symmetry upon
and that neither one changes with z.
[I am using r rather than the textbook's s for the radial direction.]
Meanwhile each of the conductors is at constant potential,
forcing cylindrical symmetry upon 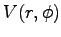 through its boundary conditions.
This symmetry is passed on to
through its boundary conditions.
This symmetry is passed on to
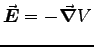 ,
so there can be no aximuthal component of
,
so there can be no aximuthal component of 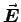 :
: 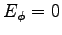 and
and 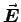 is radial everywhere. .
[Note that this does not mean a uniform distribution of
surface charge on the conductors! See next part.]
is radial everywhere. .
[Note that this does not mean a uniform distribution of
surface charge on the conductors! See next part.]
- Deduce the capacitance per unit length of this coaxial capacitor.
ANSWER: A capacitor filled with a dielectric has a larger surface charge
on the conductors for the same electric field in between
(i.e. the same voltage across) so its capacitance is increased
by a factor of
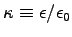 (the dielectric constant,
written "
(the dielectric constant,
written "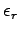 " in the textbook).
More charge will pile up on the conductors
where the dielectric is than elsewhere;
" in the textbook).
More charge will pile up on the conductors
where the dielectric is than elsewhere;
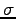 will be uniform within each region,
but a factor of
will be uniform within each region,
but a factor of 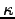 higher where the
space is filled with dielectric.
The net capacitance is the average
of what one would get for the empty capacitor
and what one would get if it were completely filled:
higher where the
space is filled with dielectric.
The net capacitance is the average
of what one would get for the empty capacitor
and what one would get if it were completely filled:
![\fbox{ ${\displaystyle {C \over L}
= {2\pi \over \ln\left(b/a\right)}\left[\ep . . .
. . . \epsz \over 2\right]
= {\pi \epsz (\kappa + 1) \over \ln\left(b/a\right)} }$}](img70.gif)
- If the conductors carry free charges per unit length
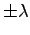 ,
find the polarization
,
find the polarization 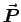 in the dielectric
at any point a distance r from the central axis, in terms of
in the dielectric
at any point a distance r from the central axis, in terms of
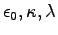 and r.
ANSWER: We have
and r.
ANSWER: We have
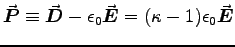 .
From Gauss' law on a cylinder of length
.
From Gauss' law on a cylinder of length 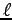 and radius r
(with a<r<b) we have
and radius r
(with a<r<b) we have
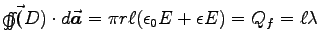 .
Thus
.
Thus
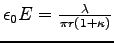 ,
giving
,
giving
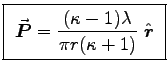 .
.
- LINEAR CURRENTS:
Two very long parallel wires carry equal currents
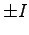 in opposite directions, as illustrated in the figure.
Take the
in opposite directions, as illustrated in the figure.
Take the 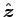 direction to be out of the page,
in the direction of the current in wire 1.
The field point P is located a distance r1 from wire 1
and a distance r2 from wire 2, as shown.
direction to be out of the page,
in the direction of the current in wire 1.
The field point P is located a distance r1 from wire 1
and a distance r2 from wire 2, as shown.
- Consider each wire separately and indicate the direction
of the vector potential
 in each case.
ANSWER:
Generally
in each case.
ANSWER:
Generally
For thin wires we can replace the volume integral by a line integral:
where it is usually assumed that the current loop is closed.
In this case we pretend it is not, and take one wire at a time,
choosing the origin at point P for simplicity ( ).
Since
).
Since
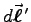 is everywhere parallel to
is everywhere parallel to 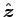 ,
at point P
,
at point P
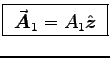 and
and
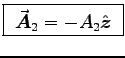 .
.
- Show that the vector potential
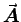 at the point P
is given by:
at the point P
is given by:
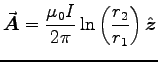 ANSWER: Choose the zero of
ANSWER: Choose the zero of 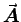 arbitrarily at some radius R
from the wire of your choice. If we construct a rectangular loop
with sides of length
arbitrarily at some radius R
from the wire of your choice. If we construct a rectangular loop
with sides of length 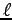 parallel to the wire (along
parallel to the wire (along 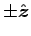 )
and the other sides radial from r<R out to R, the magnetic flux
through that loop,
)
and the other sides radial from r<R out to R, the magnetic flux
through that loop,
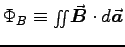 around that loop is equal (since
around that loop is equal (since
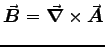 ) to
) to
 by Stokes' theorem.
We know
by Stokes' theorem.
We know
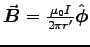 so
so
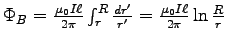 .
Meanwhile, since two sides are
.
Meanwhile, since two sides are 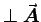 and one of the others is
at R where
and one of the others is
at R where 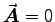 , the line integral of
, the line integral of
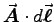 is just
is just 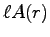 . Setting these equal gives
. Setting these equal gives
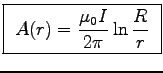 for the wire of your choice.
The total
for the wire of your choice.
The total 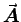 is the sum of
is the sum of
![$\Vec{A}_1 + \Vec{A}_2
= [A(r_1) - A(r_2)]\Hat{z}
= {\muz I \over 2\pi} \left[\ln{R \over r_1} - \ln{R \over r_2}\right] \Hat{z}$](img101.gif) or
or
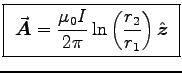 .
.
- Show that the result in part (b) is consistent with
that obtained using Ampère's law.
ANSWER: Treat the wires separately. For the wire of your choice,
in cylindrical coordinates (again using r instead of s)
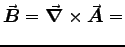
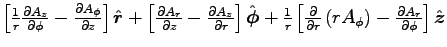 but
but
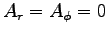 and
and
 , so
, so
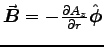 , or
, or
![$\Vec{B} = - {\muz I \over 2\pi}\DbyD{}{r}\left[
\ln R - \ln r\right] \Hat{\phi}$](img108.gif) , or
, or
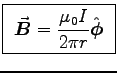
for each wire, the same as we get from AMPÈRE'S LAW.
(Note: since each wire's 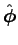 is different, the net field
is messy looking; that's why we just did it one at a time, relying
on the knowledge that we can superimpose them if needed.
Also note: the derivation of
is different, the net field
is messy looking; that's why we just did it one at a time, relying
on the knowledge that we can superimpose them if needed.
Also note: the derivation of  used the
used the  above,
supplied by AMPÈRE'S LAW, so consistency is hardly surprising!)
above,
supplied by AMPÈRE'S LAW, so consistency is hardly surprising!)
- LAPLACE'S EQUATION:
Consider an infinitely long metal pipe, of radius R,
which is placed at right angles to
an otherwise uniform electric field
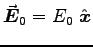 .
.
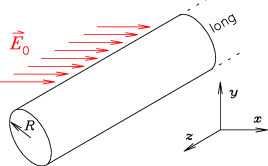
Hint: Note that this situation has cylindrical symmetry (not spherical!),
with no z dependence, and hence simplifies to a 2-D plane polar problem.
- What is the "uniqueness theorem"
and why would you want to use it to solve for
the electric potential V?
ANSWER: The UNIQUENESS THEOREM says that if you have a
solution
 of Poisson's (or Laplace's) equation in some region
and it has the right values at all the boundaries of that region,
then it is the only solution in that region. It's obvious why
this is desirable: you can guess, and if it works, it's right!
Of course, educated guesses are a lot more efficient, and so we check
our list of all possible solutions for the specified
symmetry imposed by the boundary conditions. This quickly
eliminates all the really dumb gueses. Then we take advantage of the
linearity of the differential equation for V, which ensures that
any linear combination of the above list is allowed. Usually from there
we just have to find the constants that make it fit at the boundaries.
What's not to like?
of Poisson's (or Laplace's) equation in some region
and it has the right values at all the boundaries of that region,
then it is the only solution in that region. It's obvious why
this is desirable: you can guess, and if it works, it's right!
Of course, educated guesses are a lot more efficient, and so we check
our list of all possible solutions for the specified
symmetry imposed by the boundary conditions. This quickly
eliminates all the really dumb gueses. Then we take advantage of the
linearity of the differential equation for V, which ensures that
any linear combination of the above list is allowed. Usually from there
we just have to find the constants that make it fit at the boundaries.
What's not to like?
- What are the boundary conditions on the electric potential V?
ANSWER: Let's measure r from the axis of the cylinder
and set
 in the
in the 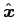 direction.
The surface of the conductor at r = R must be an equipotential
(which we are free to set equal to zero),
direction.
The surface of the conductor at r = R must be an equipotential
(which we are free to set equal to zero),
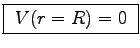 independent of
independent of  , but far from the cylinder
, but far from the cylinder
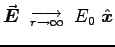 so that
so that
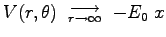 or
or
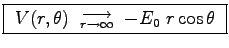 .
.
- Solve Laplace's equation for the potential V
outside the long metal pipe. You should obtain:
 .
ANSWER: The most general form has all integer powers of
.
ANSWER: The most general form has all integer powers of 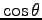 and
and 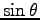 , but the boundary condition at
, but the boundary condition at 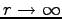 tells us immediately that we need only use n=1 with
tells us immediately that we need only use n=1 with 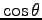 and correspondingly only r or 1/r (or both) for the r-dependence.
The most general reasonable solution is thus
and correspondingly only r or 1/r (or both) for the r-dependence.
The most general reasonable solution is thus
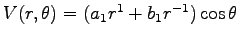 .
Let's see if we can find values for a1 and b1 that satisfy the
boundary conditions. As
.
Let's see if we can find values for a1 and b1 that satisfy the
boundary conditions. As 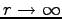 we can ignore the effect of
the second term, leaving simply a1 = -E0. Good so far.
How about
we can ignore the effect of
the second term, leaving simply a1 = -E0. Good so far.
How about
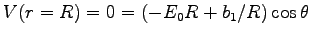 ?
This can only be true if b1/R = E0 R or b1 = E0 R2.
Hey, we're done!
?
This can only be true if b1/R = E0 R or b1 = E0 R2.
Hey, we're done!
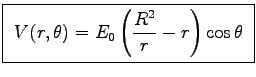 .
.



Jess H. Brewer
2006-01-12
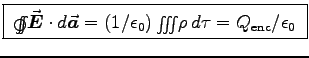 .
Similarly for
.
Similarly for 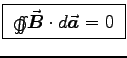 .
We use (5) [also known as the CURL THEOREM]
on
.
We use (5) [also known as the CURL THEOREM]
on 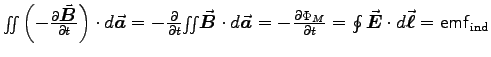 or
or
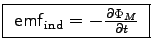 .
Finally we apply (5) to
.
Finally we apply (5) to 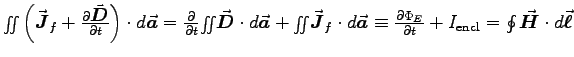 or
or
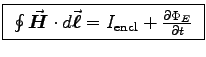 .
.
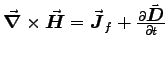 , derive the continuity equation,
, derive the continuity equation, 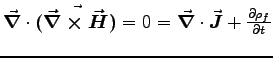 which is the same
as the CONTINUITY EQUATION if we note that
which is the same
as the CONTINUITY EQUATION if we note that
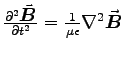 or
or
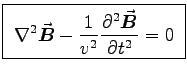
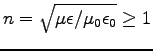 is the index of refraction.
is the index of refraction.
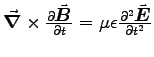 .
Then we take the curl of Eq. (2) to get
.
Then we take the curl of Eq. (2) to get
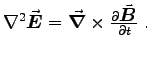 Again matching up RHS with LHS gives
Again matching up RHS with LHS gives
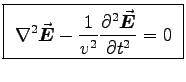

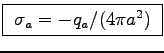 and
and
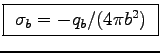 .
The net interior surface charge, -(qa+qb), leaves behind a
charge +(qa+qb) which will distribute itself uniformly over
the outer surface (to achieve maximum separation), giving an
exterior surface charge of
.
The net interior surface charge, -(qa+qb), leaves behind a
charge +(qa+qb) which will distribute itself uniformly over
the outer surface (to achieve maximum separation), giving an
exterior surface charge of
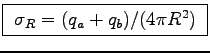 .
.
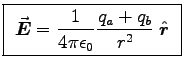 .
.
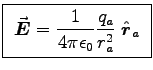 and
and
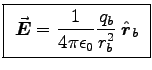 ,
where ra and rb are the distances from the centre of each cavity,
respectively.
,
where ra and rb are the distances from the centre of each cavity,
respectively.

![\fbox{ ${\displaystyle {C \over L}
= {2\pi \over \ln\left(b/a\right)}\left[\ep . . .
. . . \epsz \over 2\right]
= {\pi \epsz (\kappa + 1) \over \ln\left(b/a\right)} }$}](img70.gif)
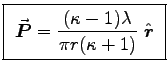 .
.

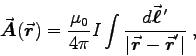
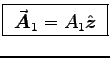 and
and
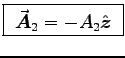 .
.
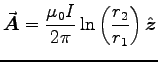 ANSWER: Choose the zero of
ANSWER: Choose the zero of 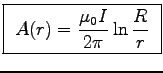 for the wire of your choice.
The total
for the wire of your choice.
The total 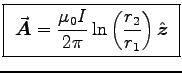 .
.
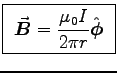

 .
ANSWER: The most general form has all integer powers of
.
ANSWER: The most general form has all integer powers of 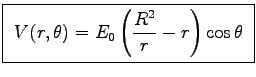 .
.