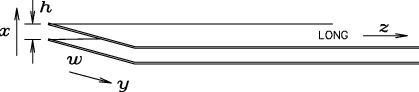
- Find the capacitance per unit length,
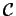 .
ANSWER: We have a parallel-plate capacitor
with a plate separation d=h and an area
.
ANSWER: We have a parallel-plate capacitor
with a plate separation d=h and an area 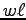 ,
where
,
where 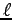 is the length of the strip.
Thus
is the length of the strip.
Thus
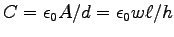 and
and
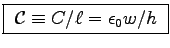 .
.
- Find the inductance per unit length,
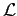 .
ANSWER: Assuming the current flows to the right (
.
ANSWER: Assuming the current flows to the right ( )
on the bottom strip and back (
)
on the bottom strip and back (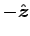 ) on the top,
AMPÈRE'S LAW gives
) on the top,
AMPÈRE'S LAW gives
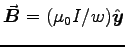 (uniform between the strips, zero elsewhere).
For a length
(uniform between the strips, zero elsewhere).
For a length  the resultant flux is
the resultant flux is
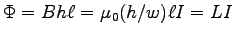 , so
, so
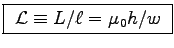 .
.
- What is the product,
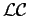 , numerically?
1ANSWER:
, numerically?
1ANSWER:
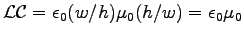 or
or
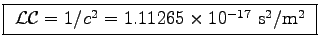 .
.
- If the strips are insulated from one another by
a nonconducting material of permittivity
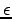 and permeability
and permeability 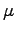 , what is then the product
, what is then the product 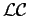 ?
What is the propagation speed?
2ANSWER: We simply replace
?
What is the propagation speed?
2ANSWER: We simply replace 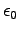 by
by 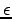 and
and 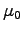 by
by 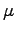 ,
giving
,
giving
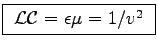
where v < c is the propagation velocity of a pulse down the line.
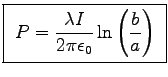 .
.
Is this the same as VI? We have
For Problem 7.58,
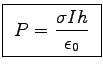 .
.
Compare
- Determine all nine elements of the stress tensor
in the region between the plates.
Display your answer as a 3 x 3 matrix:
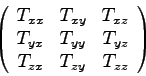
ANSWER: Generally
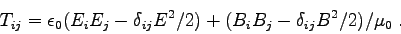
In this case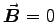 and
and
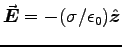 has only one component (Ez), so all off-diagonal terms are zero and
has only one component (Ez), so all off-diagonal terms are zero and
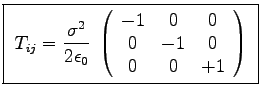 .
.
- Use Eq. (8.22) on p. 353 to determine
the force per unit area on the top plate.
Compare Eq. (2.51) on p. 103.
ANSWER: Since
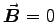 ,
, 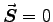 , leaving
, leaving
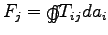 .
A surface enclosing both plates will yield a zero result,
since there is no field outside the capacitor. What we want is
a surface enclosing just the top plate.
Its shape above the plate where
.
A surface enclosing both plates will yield a zero result,
since there is no field outside the capacitor. What we want is
a surface enclosing just the top plate.
Its shape above the plate where 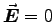 doesn't matter,
but inside the gap it should be normal to
doesn't matter,
but inside the gap it should be normal to 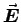 and parallel
to the plate - i.e.
and parallel
to the plate - i.e.
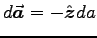 (remember,
(remember,
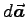 always points out of the enclosed region).
Thus Eq. (8.22) is reduced to
always points out of the enclosed region).
Thus Eq. (8.22) is reduced to
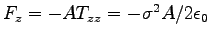 and
and
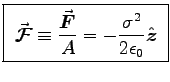 ,
,
in agreement with Eq. (2.51). - What is the momentum per unit area, per unit time,
crossing the xy plane (or any other plane parallel to that one,
between the plates)?
ANSWER: Really this is just a question of momentum conservation.
The upper plate feels a downward force (and the lower plate an
equal and opposite upward one); this force is transmitted
by the electric field: you may think of the lower plate
"emitting" an electromagnetic field with momentum flux
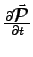 per unit area and time,
and the upper plate "absorbing" same:
per unit area and time,
and the upper plate "absorbing" same:
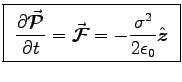 .
.
- At the plates this momentum is absorbed, and the plates recoil
(unless there is some other force holding them in position).
Find the recoil force per unit area on the top plate,
and compare your answer to that in part (b).
3ANSWER: It's the same thing, we already said that.
There are two conceptual challenges to this picture:
First, we are not used to "things" whose momentum is toward
their emitter and away from their absorber. Switching the
roles of the two plates is no help; the same conundrum persists.
Second, we have already noted that
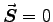 (no magnetic field).
So the momentum is not being transmitted as a Poynting vector.
It is in the stress tensor itself (see p. 356).
(By asking the same question three times in different guises,
Griffiths is trying to force you to reconcile these notions
in your own mind. I hope it worked. :-)
(no magnetic field).
So the momentum is not being transmitted as a Poynting vector.
It is in the stress tensor itself (see p. 356).
(By asking the same question three times in different guises,
Griffiths is trying to force you to reconcile these notions
in your own mind. I hope it worked. :-)
- Calculate Ir in terms of dIS/dt.
ANSWER: We have within the solenoid a uniform magnetic field
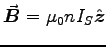 , giving a flux
, giving a flux
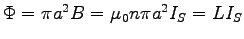 in the positive z direction.
If IS decreases, a current
in the positive z direction.
If IS decreases, a current
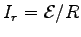 will flow in such a
direction as to replace the missing flux - i.e. in the same
sense as the original current in the solenoid.
Here
will flow in such a
direction as to replace the missing flux - i.e. in the same
sense as the original current in the solenoid.
Here
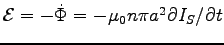 ,
so that
,
so that
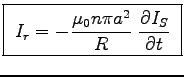 .
.
- The power (Ir2 R) delivered to the ring
must have come from the solenoid. Confirm this by
calculating the Poynting vector just outside the solenoid, where
the electric field is due to the changing flux in the solenoid
and the magnetic field is due to the current in the ring.
Integrate over the entire surface of the solenoid, and check that
you recover the correct total power.
ANSWER: In the above calculation
(which required only first year Physics methods)
we were careful not to mix up the "cause"
(the changing magnetic field of the solenoid) with the "effect"
(the magnetic field generated by Ir in the ring).
But when we think in terms of "the electromagnetic field"
in calculating the Poynting vector (or, for that matter,
the stress tensor) there is no such separation: we must use
the total field(s) at any given time.
Outside the solenoid there is no
 from the solenoid itself,
but the current in the ring generates a field
from the solenoid itself,
but the current in the ring generates a field
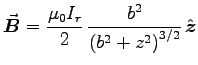 (see Example 5.6 on p. 218). Meanwhile
(see Example 5.6 on p. 218). Meanwhile
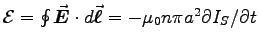 ,
and (by symmetry)
,
and (by symmetry)
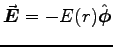 ,
so around any loop at r we have
,
so around any loop at r we have
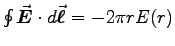
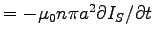 , giving
, giving
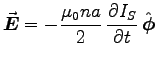 .
Putting these together gives
.
Putting these together gives
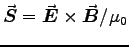
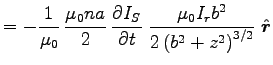 .
Using the earlier result we can substitute
.
Using the earlier result we can substitute
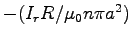 for
for 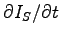 to get
to get
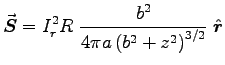 .
Now we integrate
.
Now we integrate
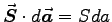 over the surface of the solenoid to get the net power P
"sent" to the ring:
over the surface of the solenoid to get the net power P
"sent" to the ring:
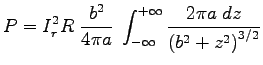
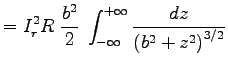 .
Looking up the integral (http://integrals.wolfram.com/index.jsp
is a big help!) we have
.
Looking up the integral (http://integrals.wolfram.com/index.jsp
is a big help!) we have
![${\displaystyle \int_{-\infty}^{+\infty}
{dz \over \left(b^2 + z^2\right)^{3/2 . . .
. . . b^2 \left(b^2 + z^2\right)^{1/2}\right]_{-\infty}^{+\infty}
= {2 \over b^2} }$](img73.gif) , giving
, giving
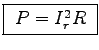 .
.
(This sure is doing it the hard way, but it's nice to know that really is transmitting power.)
really is transmitting power.)
- Calculate the power you'd need to produce 1 Newton
of thrust with a photon drive rocket. How does this compare with
the typical output of BC's huge Stave Lake power station,
which has a peak capacity of about 200 MW?
ANSWER: We did something like this in class: if
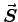 is power
per unit area and
is power
per unit area and 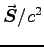 is momentum density per unit volume,
then
is momentum density per unit volume,
then 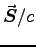 is the "radiation pressure" (force per unit area)
and the relationship between net force F and net power P is just
F = P/c. So for a 1 N thrust you'd need about 3 x 108 W or
is the "radiation pressure" (force per unit area)
and the relationship between net force F and net power P is just
F = P/c. So for a 1 N thrust you'd need about 3 x 108 W or
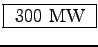 . Stave Lake could manage 2/3 N.
. Stave Lake could manage 2/3 N.
- What accelerations would result if your power source provided
200 MW and the total mass of the rocket were 20,000 kg?
ANSWER: From
a = F/m = 2/(3 x 2 x 104) we get
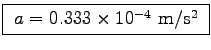 . Pretty puny.
. Pretty puny.
- In spite of these numbers, the photon drive offers one very attractive advantage over conventional rockets, especially for long space voyages. What is it? ANSWER: It keeps going and going and going and . . . . If it weren't for relativity, we would reach c after only 285,000 years! Hmm, maybe if we use antimatter annihilation . . . .