- Suppose you embedded some free charge in a piece of glass.
About how long would it take for the charge to flow to the surface?
ANSWER:
We know charge density dissipates exponentially in a conductor
according to
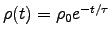 where
where
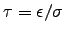 .
It's strange to think of glass as a conductor,
but no insulator is perfect.
Different glasses have a wide range of resistivities,
from 1010 to 1014
.
It's strange to think of glass as a conductor,
but no insulator is perfect.
Different glasses have a wide range of resistivities,
from 1010 to 1014 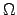 -m
(even 1016 for fused quartz, which most people would consider
a type of glass). Since
-m
(even 1016 for fused quartz, which most people would consider
a type of glass). Since
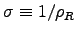 (I'm using
(I'm using 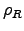 to denote resistivity here),
that means
to denote resistivity here),
that means 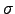 (the conductivity) has a range from
10-14 to 10-10
(the conductivity) has a range from
10-14 to 10-10 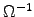 m-1
(10-16 for fused quartz). Table 4.2 doesn't list
glass or quartz, but we can assume they have
m-1
(10-16 for fused quartz). Table 4.2 doesn't list
glass or quartz, but we can assume they have
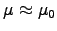 and therefore
and therefore
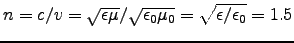 or
or
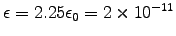 C2/N-m2.
Thus
C2/N-m2.
Thus
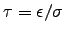 is
is
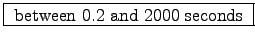 for "glass" and as long as 200,000 seconds (2.3 days!) for fused quartz.
for "glass" and as long as 200,000 seconds (2.3 days!) for fused quartz.
- Silver is an excellent conductor, but it's expensive.
Suppose you were designing a microwave experiment to operate
at a frequency of 1010 Hz.
How thick would you make the silver coatings?
ANSWER:
The skin depth is
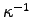 , where
, where
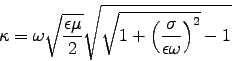
is the imaginary part of the wavevector. For Ag, we have2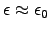 ,
,
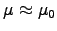 (so that
(so that
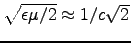 ),
and
),
and
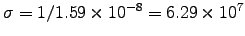
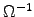 m-1.
Thus, for
m-1.
Thus, for
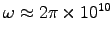 s-1,
we expect
s-1,
we expect
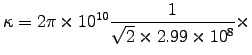
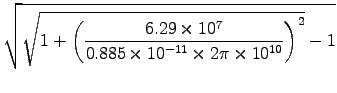
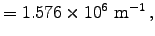 giving a skin depth of
giving a skin depth of
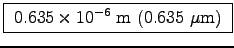 .
Thus only 20.7% of the original electric field strength in a
1010 Hz microwave signal will penetrate a silver film
1
.
Thus only 20.7% of the original electric field strength in a
1010 Hz microwave signal will penetrate a silver film
1 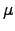 m (one micron) thick. You may want a thicker film
to get really thorough reflection.
m (one micron) thick. You may want a thicker film
to get really thorough reflection.
- Find the wavelength and propagation speed in copper
for radio waves at 1 MHz.
Compare the corresponding values in air (or vacuum).
ANSWER:
For Cu we have
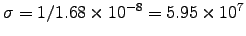
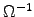 m-1.
Again we assume
m-1.
Again we assume
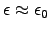 and
and
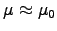 ,
so for
,
so for
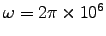 s-1 we have
s-1 we have
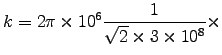
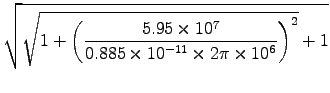 = 1.53 x 104 m
= 1.53 x 104 m
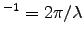 , so
, so
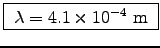 (0.41 mm or 410
(0.41 mm or 410 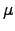 m).
The corresponding vacuum value at that frequency would be
much larger:
m).
The corresponding vacuum value at that frequency would be
much larger:
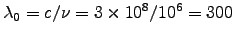 m.
m.
- Show that the skin depth in a poor conductor
(
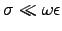 ) is
) is
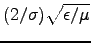 (independent of frequency).
Find the skin depth (in meters) for (pure) water.3ANSWER:
For
(independent of frequency).
Find the skin depth (in meters) for (pure) water.3ANSWER:
For
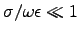 we can approximate
we can approximate
![$\left[1 + (\sigma/\epsilon\omega)^2\right]^{1/2}
\approx 1 + (1/2)(\sigma/\epsilon\omega)^2$](img33.gif) ,
giving
,
giving
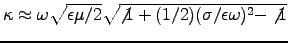
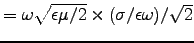 or
or
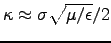 , so
, so
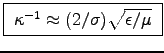 .
.
For pure water,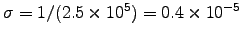
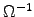 m-1,
m-1,
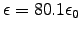 and
and
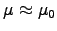 , so it's a poor conductor with a skin depth
of
, so it's a poor conductor with a skin depth
of
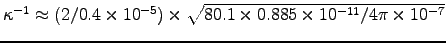
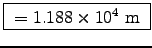 (about 12 km).4
(about 12 km).4
- Show that the skin depth in a good conductor
(
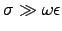 ) is
) is 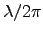 (where
(where 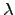 is the wavelength in the conductor.
Find the skin depth (in nanometers) for a typical metal
[
is the wavelength in the conductor.
Find the skin depth (in nanometers) for a typical metal
[
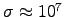 (
(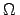 m)-1]
in the visible range (
m)-1]
in the visible range (
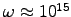 s-1),
assuming
s-1),
assuming
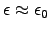 and
and
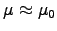 .
Why are metals opaque?
ANSWER:
In a good conductor,
.
Why are metals opaque?
ANSWER:
In a good conductor,
 , so
, so
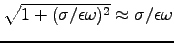 and
and
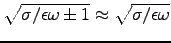 , giving
, giving
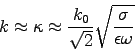
where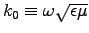 is the wavevector
of an insulator with the same
is the wavevector
of an insulator with the same 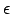 and
and 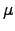 .
Since
.
Since
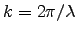 and
and
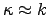 ,
it follows that the skin depth
,
it follows that the skin depth
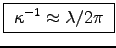 .
For
.
For
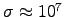
 m-1
and
m-1
and
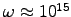 s-1,
s-1,
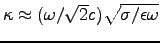 = (1015/1.414 x 3 x 108) x
= (1015/1.414 x 3 x 108) x
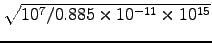 = 7.93 x 107 m(-1) and so the skin depth is
= 7.93 x 107 m(-1) and so the skin depth is
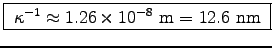 .
This is only a few atomic layers. How opaque can you get?
.
This is only a few atomic layers. How opaque can you get?
- Show that in a good conductor the magnetic field
lags the electric field by 45
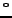 ,
and find the ratio of their amplitudes.
For a numerical example, use the "typical metal"
in the previous question.
ANSWER:
From Faraday's law we have
,
and find the ratio of their amplitudes.
For a numerical example, use the "typical metal"
in the previous question.
ANSWER:
From Faraday's law we have
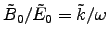 ,
where
,
where
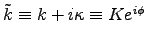 ,
,
![${\displaystyle K = \vert\tilde{k}\vert = \sqrt{k^2 + \kappa^2}
= {\omega \over c}
\left[1 + \left(\sigma\over\epsilon\omega\right)^2\right]^{1/4} }$](img63.gif) and
and
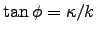 . Since
. Since
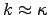 (see previous part),
(see previous part),
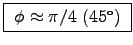 .
All we need is
.
All we need is
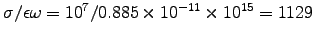 to get
to get
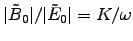
![$= \left[1 + (1129)^2\right]^{1/4}/3\times10^8$](img69.gif) or
or
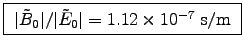 .
.
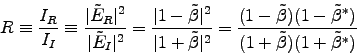
where
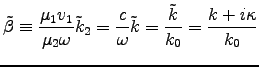 .
It's tempting to use the approximation in the previous problem
to set
.
It's tempting to use the approximation in the previous problem
to set
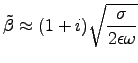 for a good conductor like silver.
However, this leads to a result
for a good conductor like silver.
However, this leads to a result
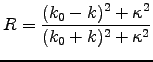 .
.
If we define
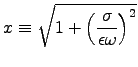 ,
then
,
then
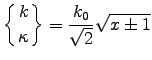 ,
giving
,
giving
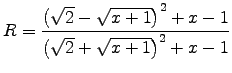
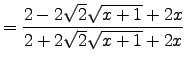
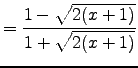 ,
at which point we can plug in numbers:
assuming
,
at which point we can plug in numbers:
assuming
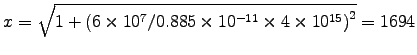 and so
and so
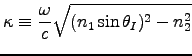 and
and
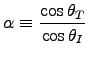 is now imaginary, use Eqs. (9.109),
is now imaginary, use Eqs. (9.109),
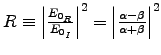 where
where
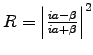 where a and
where a and 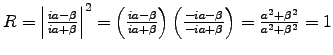 .
.
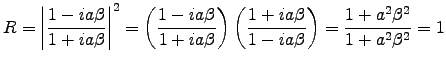 .
.
![\begin{eqnarray*}
\Vec{E}(\Vec{r},t) &=& E_0 \; e^{-\kappa z}
\cos (kx - \ome . . .
. . . t) \; \Hat{x}
+ \; k \cos (kx - \omega t) \; \Hat{z} \, ] \; .
\end{eqnarray*}](img124.gif)
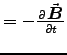
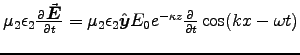
![\fbox{ ${\displaystyle \Vec{S} =
{E_0^2 \over \omega\mu_2} e^{-2\kappa z} \lef . . .
. . . x} \, - \,
\kappa \sin(kx-\omega t) \cos(kx-\omega t) \; \Hat{z} \right] }$\ }](img154.gif) .
Time averages are
.
Time averages are
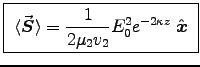 .
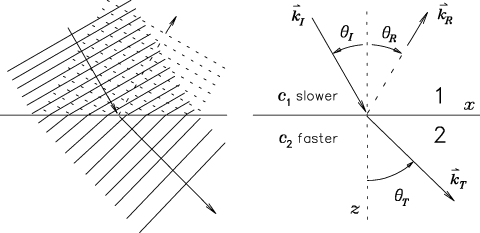
As predicted, there is no net energy flow in the z direction,
only in the x direction parallel to the surface of the interface.
.
As predicted, there is no net energy flow in the z direction,
only in the x direction parallel to the surface of the interface.