(p. 411, Problem 9.27) - No TE00:
Show that the mode TE00 cannot occur in a rectangular wave guide.
[Hint: In this case 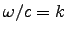 , so Eqs. (9.180) are indeterminate,
and you must go back to Eqs. (9.179). Show that Bz is a constant,
and hence - applying Faraday's law in integral form to a cross section -
that Bz = 0, so this would be a TEM mode.]
, so Eqs. (9.180) are indeterminate,
and you must go back to Eqs. (9.179). Show that Bz is a constant,
and hence - applying Faraday's law in integral form to a cross section -
that Bz = 0, so this would be a TEM mode.]
ANSWER:
From the definition of the mode numbers m and n, a TE00 mode
would have kx = ky = 0 - i.e. we'd have an ordinary plane wave
propagating straight down the waveguide at c.
Neither 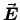 nor
nor 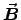 would depend on x or y
within the guide, only on z and t.
Both would be perpendicular to
would depend on x or y
within the guide, only on z and t.
Both would be perpendicular to
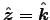 ;
like the sides of the guide, one would be parallel to
;
like the sides of the guide, one would be parallel to 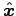 and the other would be parallel to
and the other would be parallel to 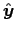 .
Thinking in these terms, we can see several reasons why such a wave
is impossible. The most obvious is that
if
.
Thinking in these terms, we can see several reasons why such a wave
is impossible. The most obvious is that
if
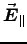 does not depend on x or y,
there is no way for it to change continuously to zero
inside the conductor, as it must. The same applies to
does not depend on x or y,
there is no way for it to change continuously to zero
inside the conductor, as it must. The same applies to 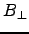 .
However, we are not encouraged by Griffiths to visualize the wave as
a superposition of reflections (or, in this case, no
reflections) of a simple plane wave; in principle there might
be some exotic (x,y) dependence that would keep kx = ky = 0
and still satisfy MAXWELL'S EQUATIONS, so we go the formal route
and prove otherwise.
.
However, we are not encouraged by Griffiths to visualize the wave as
a superposition of reflections (or, in this case, no
reflections) of a simple plane wave; in principle there might
be some exotic (x,y) dependence that would keep kx = ky = 0
and still satisfy MAXWELL'S EQUATIONS, so we go the formal route
and prove otherwise.
For any TE wave, Ez = 0 by definition. Equations (9.179) then become
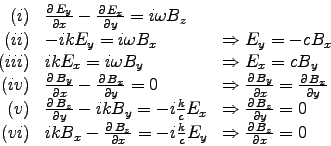
The last two results show that Bz is independent of x or y,
i.e. constant over any x-y plane.
Thus if we apply the integral form of FARADAY'S LAW
over a loop in any x-y plane just inside the metal of the guide
(where E = 0), we get
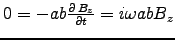
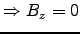 , i.e. the wave is also a TM wave,
so it is a TEM mode, which was shown at the bottom of p. 407
to be impossible in a hollow waveguide.
, i.e. the wave is also a TM wave,
so it is a TEM mode, which was shown at the bottom of p. 407
to be impossible in a hollow waveguide.
![\begin{displaymath}
\tVec{E}(z,t) = \tilde{E}_0 \, e^{-\kappa z} \, e^{i(kz-\om . . .
. . . \over \omega_j^2 - \omega^2 - i \gamma_j \omega} \right] \; .
\end{displaymath}](img3.gif)
![]() makes
makes
![]() pure real,
simplifying matters considerably.
We can just invert the derivative:
pure real,
simplifying matters considerably.
We can just invert the derivative:
![]() so first we find
so first we find
![\begin{eqnarray*}
{dk \over d\omega} &=& {1 \over c} \left( 1 + {N q^2 \over 2 . . .
. . . 2 \over
\left(\omega_j^2 - \omega^2\right)^2} \right] \right)
\end{eqnarray*}](img7.gif)
![\fbox{ ${\displaystyle v_g = c \; \left[
1+{Nq^2 \over 2m\epsz} \sum_j {(\omega . . .
. . . + \omega^2)f_j \over
\left(\omega_j^2 + \omega^2\right)^2 } \right]^{-1} }$\ }](img8.gif) .
.
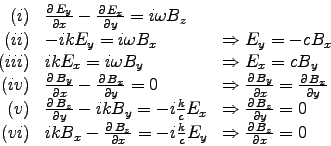
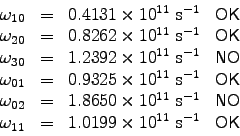
 and
and
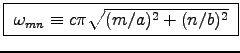 ,
and the dispersion relation,
,
and the dispersion relation,
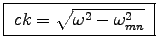 ,
from which it is obvious that unless
,
from which it is obvious that unless
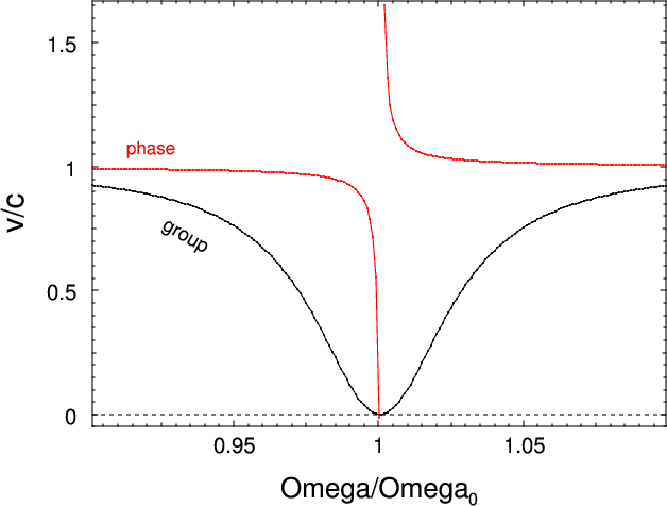
![\fbox{ $v_{\rm ph} \equiv \omega/k
= c \left[1 - (\omega_{mn}/\omega)^2\right]^{-1/2}$\ }](img41.gif) and the group velocity is
and the group velocity is
![\fbox{ $v_g = c \left[1 - (\omega_{mn}/\omega)^2\right]^{1/2}$\ }](img42.gif) just as for TE modes.
The lowest TM cutoff frequency is
just as for TE modes.
The lowest TM cutoff frequency is  .
.