can be expressed in "coordinate-free" form by writing
ANSWER:
![\fbox{ ${\displaystyle V = - {\omega \over 4\pi\epsz c}
\left(\Vec{p}_0\cdot\Hat{r}\over r\right)
\sin\left[\omega\left(t - {r \over c}\right)\right]
}$\ }](img3.gif) . . . and similarly for Equation (11.17),
. . . and similarly for Equation (11.17),
ANSWER:
![\fbox{ ${\displaystyle
\Vec{A} = - {\muz \Vec{p}_0 \omega \over 4\pi r}
\sin\left[\omega\left(t - {r \over c}\right)\right]
}$\ }](img5.gif) . . . Equation (11.18),
. . . Equation (11.18),
![\begin{displaymath}
\Vec{E}(r,\theta,t) = - {\muz p_0 \omega^2 \over 4\pi}
\l . . .
. . . ft[\omega\left(t - {r \over c}\right)\right] \Hat{\theta} \, ,
\end{displaymath}](img6.gif)
ANSWER:
![\fbox{ ${\displaystyle
\Vec{E} = {\muz \omega^2 \over 4\pi}
\left((\Hat{r} \ . . .
. . . at{r} \over r\right)
\cos\left[\omega\left(t - {r \over c}\right)\right]
}$\ }](img7.gif) . . . Equation (11.19),
. . . Equation (11.19),
![\begin{displaymath}
\Vec{B}(r,\theta,t) = - {\muz p_0 \omega^2 \over 4\pi c}
. . .
. . . left[\omega\left(t - {r \over c}\right)\right] \Hat{\phi} \, ,
\end{displaymath}](img8.gif)
ANSWER:
![\fbox{ ${\displaystyle
\Vec{B} = {\muz \omega^2 \over 4\pi c}
\left(\Hat{r} . . .
. . . {p}_0 \over r\right)
\cos\left[\omega\left(t - {r \over c}\right)\right]
}$\ }](img9.gif) . . . and Equation (11.21),
. . . and Equation (11.21),
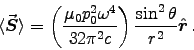
ANSWER: As always,
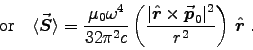
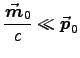 for an atom with magnetic dipole moment
for an atom with magnetic dipole moment
- In terms of the variables given
(not all of which may be relevant, of course)
find the formula for the intensity of the radiation at ground level,
a distance R away from the base of the tower.
You may assume that
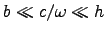 .
[Note: we are interested only in the magnitude
of the radiation, not in its direction -
when measurements are taken, the detector will be aimed
directly at the antenna.]
.
[Note: we are interested only in the magnitude
of the radiation, not in its direction -
when measurements are taken, the detector will be aimed
directly at the antenna.]
ANSWER: The average energy flux from a magnetic dipole antenna, Eq. (11.39), is
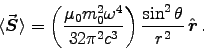
The total power radiated, Eq. (11.40), is
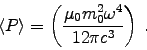
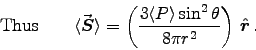
Here we have r2 = h2+R2 and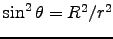 , giving
, giving
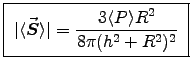 .
.
The intensity at the base of the tower (R=0) is zero, Doh! - How far from the base of the tower should the engineer
have made the measurement? What is the formula for the intensity
at this location?
ANSWER:
At the point of highest intensity, of course.
As for any extremum, this requires
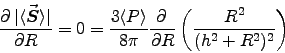
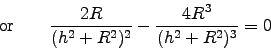
or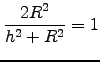 or
or
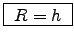 .
.
- KRUD's actual power output is 35 kilowatts,
its frequency is 90 MHz, the antenna's radius is 6 cm,
and the height of the tower is 200 m.
The city's radio-emission limit is 200 microwatts/cm2.
Is KRUD in compliance?
ANSWER:
We don't need to know
 or b. All we need is
or b. All we need is
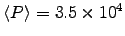 W and h=200 m.
At the point of highest intensity (at ground level),
R=h, we have
W and h=200 m.
At the point of highest intensity (at ground level),
R=h, we have
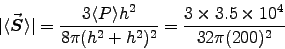
or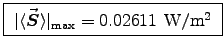
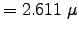 W/cm2, well within compliance.1
W/cm2, well within compliance.1
- Find the formula for the total power radiated,
in terms of the following parameters:
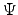 (the angle between the geographic and magnetic north poles),
M (the magnitude of the Earth's magnetic dipole moment),
and
(the angle between the geographic and magnetic north poles),
M (the magnitude of the Earth's magnetic dipole moment),
and 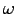 (the angular velocity of rotation of the Earth).
[Hint: refer to Prob. 11.4 or Prob. 11.12.]
(the angular velocity of rotation of the Earth).
[Hint: refer to Prob. 11.4 or Prob. 11.12.]
ANSWER: Problem 11.12 gives the total power radiated by a magnetic dipole generated by a time-varying current in a circular loop:
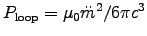 .
Problem 11.4 describes an electric dipole rotating
about the
.
Problem 11.4 describes an electric dipole rotating
about the 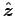 axis as a superposition of two oscillating
dipoles in the
axis as a superposition of two oscillating
dipoles in the 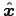 and
and 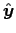 directions,
directions, 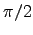 out of phase:
out of phase:
![$\Vec{p}(t) = p_0[\cos(\omega t)\Hat{x} + \sin(\omega t)\Hat{y}]$](img48.gif) .
You are then invited to find the intensity as a function of
the polar angle
.
You are then invited to find the intensity as a function of
the polar angle 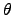 and calculate the total power radiated,
explaining why the power seems to satisfy the superposition
principle even though it is quadratic in the fields.
and calculate the total power radiated,
explaining why the power seems to satisfy the superposition
principle even though it is quadratic in the fields.
A more conventional way to represent precession of a dipole is to make the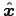 component real and the
component real and the 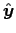 component imaginary:
component imaginary:
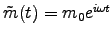 which amounts to the same thing as above. In the Earth's case
it is only the transverse component
which amounts to the same thing as above. In the Earth's case
it is only the transverse component
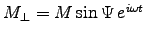 that precesses; the axial component
that precesses; the axial component
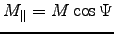 just adds a constant magnetic dipole field.
Thus
just adds a constant magnetic dipole field.
Thus
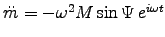 and we expect3
and we expect3
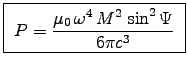 .
.
- Using the fact that the Earth's magnetic field is
about half a gauss at the Equator, estimate
the magnetic dipole moment M of the Earth.
ANSWER:
From Eq. (5.87) on p. 246 we have the field of a static magnetic dipole:
![\begin{displaymath}
\Vec{B}_{\rm dip} = {\muz\over4\pi}
\left[3(\Vec{m}\cdot\Hat{r})\Hat{r} - \Vec{m} \over r^3\right]
\end{displaymath}](img60.gif)
which reduces to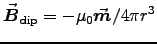 for
for
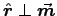 (i.e. at the Equator).
Thus
(i.e. at the Equator).
Thus
 or
or
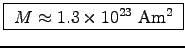 .
(We neglect the
.
(We neglect the 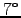 tilt and the fact that the Earth's
dipole is far from pointlike on the scale of RE.)
tilt and the fact that the Earth's
dipole is far from pointlike on the scale of RE.)
- Find the power radiated.
[Your answer should be several times 10-5 W.]
ANSWER:
The Earth's
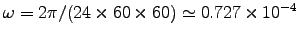 s-1.
Plugging this,
s-1.
Plugging this,
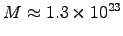 Am2,
and
Am2,
and
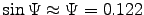 into
into
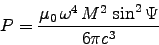
gives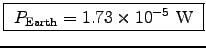 .
.
- Pulsars are thought to be rotating neutron stars,
with a typical radius of about
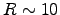 km,
a typical surface magnetic field of
km,
a typical surface magnetic field of 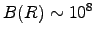 T
and a variety of rotational periods T; let's use
T
and a variety of rotational periods T; let's use 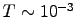 s.
What sort of radiated power would you expect from such a star?
[See J.P. Ostriker and J.E. Gunn, Astrophys. J. 157,
1395 (1969). Answer:
2 x 1036 W.]
s.
What sort of radiated power would you expect from such a star?
[See J.P. Ostriker and J.E. Gunn, Astrophys. J. 157,
1395 (1969). Answer:
2 x 1036 W.]
ANSWER: Again we use
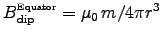 to get
to get
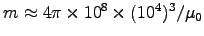 = 1027 Am2. This is only some 8000 times
bigger than the Earth's magnetic moment, but the frequency
= 1027 Am2. This is only some 8000 times
bigger than the Earth's magnetic moment, but the frequency
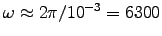 s-1 is a lot bigger,
and
s-1 is a lot bigger,
and 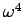 is . . . well . . . huge. Thus
(assuming the star's magnetic moment is perpendicular to its
axis of rotation, which gives the biggest result) we get
is . . . well . . . huge. Thus
(assuming the star's magnetic moment is perpendicular to its
axis of rotation, which gives the biggest result) we get
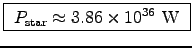 !
This is about a factor of two larger than the value
predicted by Griffiths. No doubt this is because of
the probability distribution of angles
!
This is about a factor of two larger than the value
predicted by Griffiths. No doubt this is because of
the probability distribution of angles 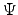 between the star's magnetic moment and its axis of rotation.
If we assume all values of
between the star's magnetic moment and its axis of rotation.
If we assume all values of 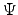 between 0 and
between 0 and 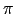 are equally likely, then we should multiply our result by
are equally likely, then we should multiply our result by
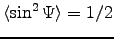 , giving
, giving
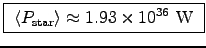 .
But this seems a little silly in two respects:
first, we are just making an estimate for a "typical"
neutron star. A 20% change of
.
But this seems a little silly in two respects:
first, we are just making an estimate for a "typical"
neutron star. A 20% change of 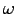 would have the same effect.
Second, it seems improbable that the formation of neutron stars
from supernovae of spinning suns would indiscriminately orient
the star's magnetic moment relative to its axis or rotation;
naively one might expect
would have the same effect.
Second, it seems improbable that the formation of neutron stars
from supernovae of spinning suns would indiscriminately orient
the star's magnetic moment relative to its axis or rotation;
naively one might expect 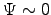 to be more likely,
which would bias our estimate toward much smaller values of
to be more likely,
which would bias our estimate toward much smaller values of
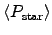 . A more realistic estimate
would require a deeper knowledge of astrophysics
than I (for one) possess.4
. A more realistic estimate
would require a deeper knowledge of astrophysics
than I (for one) possess.4